Как сделать геометрию: Геометрия с нуля – Геометрия: уроки, тесты, задания.

— многоугольники

В этой теме необходимо рассмотреть разные виды многоугольников и сумму углов n-угольника.

— теорема Пифагора

Тема, которую итак все прекрасно понимают, поэтому ничего усложнять не надо.

— площади

Здесь я опять же хочу предложить удобную схему, которую необходимо объяснять с помощью бумажных фигурок.

Трапеция опять же рассматривается отдельно.

— подобие и первый признак подобия

Рассматривается исключительно в ознакомительных целях, чтобы детям легче было понимать начала тригонометрии.

— средние линии треугольника и трапеции

Средние линии лучше рассматривать вместе, потому что так они лучше усваиваются.

— тригонометрия

В самом начала тригонометрии, школьникам стоит напомнить о том, что такое соотношения, а после очень много времени посвятить самим определениям синуса, косинуса, тангенса и котангенса, чтобы школьники понимали, откуда взялись эти странные английские буквы. Затем необходимо рассмотреть множество задач, в которых они будут использоваться. Удобнее всего давать задачи на теорему Пифагора и площади. Желательно уже на базовом уровне ознакомить детей с таблицей, т.к. сейчас они уже максимально близки к среднему и уровню и способны усваивать информацию средней сложности.

— окружность и круг

И, наконец, последняя тема на базовом уровне. Здесь необходимо напоминать детям обо всем, что связано с окружностью и кругом, начиная с определений, т.к. никто уже ничего не помнит из курса 6 класса. А также стоит рассмотреть свойство касательной, вписанный и центральный углы, и свойство гипотенузы прямоугольного треугольника.

На этом базовый курс окончен. У рядового школьника достаточно базовых знаний, на которые он мог бы опираться при решении задач, с использованием доказательств. Пришла пора поближе с ними познакомиться.

Средний уровень (доказательства)

Расписывать программу для среднего уровня смысла нет, т.к. на этом этапе ребенок готов усваивать практически любую информацию и способен аргументированно решать задачи на доказательства. Единственное, что стоит сделать, так это перечислить темы среднего уровня:

— соотношения между сторонами и углами;

— неравенство треугольника;

— признаки равенства треугольников;

— признаки подобия треугольников;

— четыре замечательные точки;

— вписанная и описанная окружности.

Этого вполне достаточно для доказательств средней степени сложности.

Высокий уровень (сложные доказательства и решение сложных задач)

К сожалению, немногие могут достичь высокого уровня, но каждый должен хотя бы попытаться. Опять же, нет смысла все подробно расписывать, поэтому будут перечислены лишь темы:

— теорема Фалеса;

— теорема Герона;

— теорема синусов;

— теорема косинусов;

— углы при окружности;

— хорды окружности;

— и т.д.

Заключение

Из всего вышесказанного можно сделать следующий вывод: прогресс любого школьника основан на его базовых знаниях. Если они есть, то их необходимо лишь грамотно развивать. Поэтому, прежде всего, необходимо упростить получение базовых знаний и сделать их максимально доступными для всех школьников без исключения.

Примечание: векторы в статье не учтены, т.к. являются дополнением ко всему вышесказанному.

Геометрия: уроки, тесты, задания.

Основы геометрии. Видеоурок. Идеи и смыслы

Математика работает с идеальными объектами. Но зачем это нужно? Возьмем два треугольника (см. рис. 1). На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая – выпуклая, а у другого наоборот (см. рис. 2).

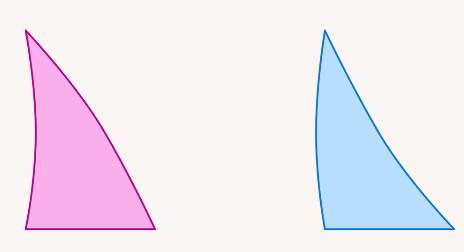
Рис. 1. Два похожих треугольника

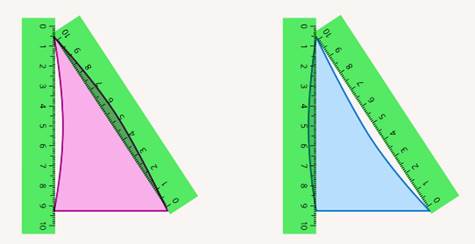
Рис. 2. Вогнутые и выпуклые стороны треугольников

Эти треугольники похожи, и, наверное, о них можно сделать близкое заключение, которое будет описывать свойства обоих. В то же время эти треугольники отличаются, что делать?

Математика занимается идеальными объектами, идеальными треугольниками (см. рис. 3) и делает о них некие заключения, которые называются теоремами (см. рис. 4). Тогда эти заключения помогут описать и первый, и второй треугольник, но с некоторыми приближениями. Чтобы вывести эти теоремы, нужно сказать, что есть идеальный объект – идеальный треугольник. Хотя, если изучать его очень подробно, он тоже будет иметь свои шероховатости (см. рис. 5). Однако мы принимаем, что есть идеальный объект – треугольник, который составлен из трех отрезков прямых (см. рис. 6).

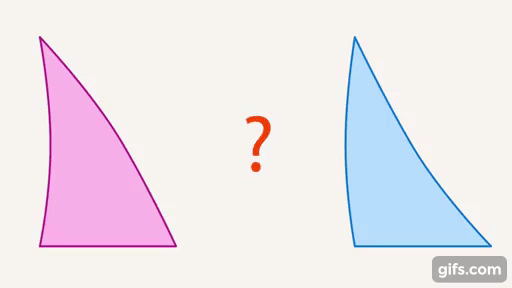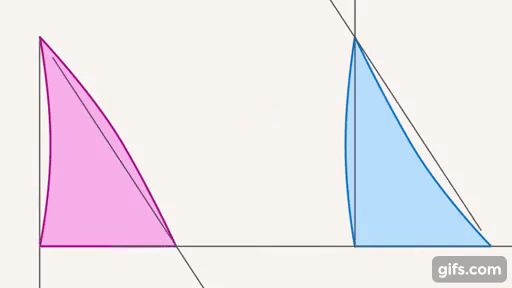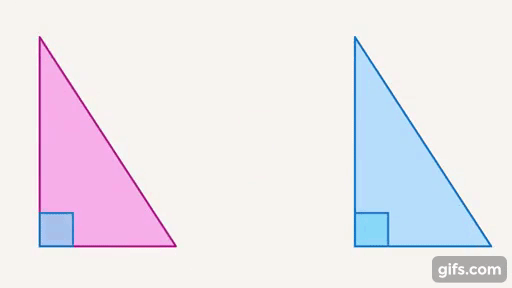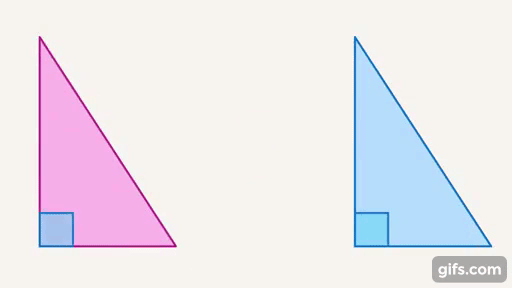
Рис. 3. Идеальные треугольники

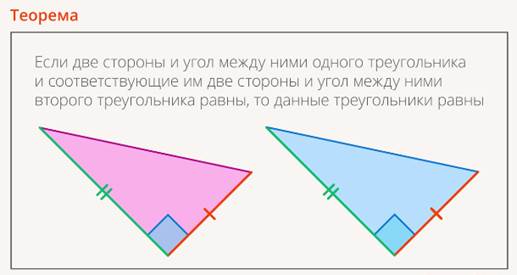
Рис. 4. Пример теоремы. Признак равенства треугольников

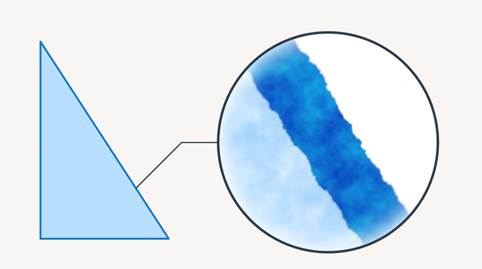
Рис. 5. Шероховатости треугольника

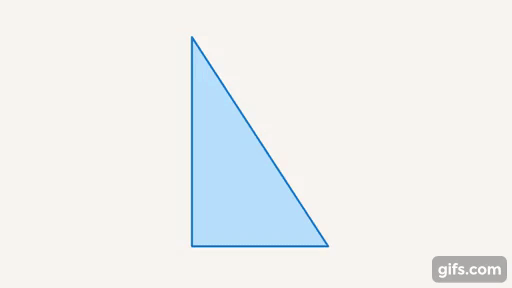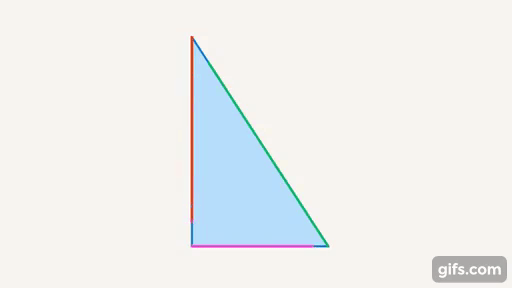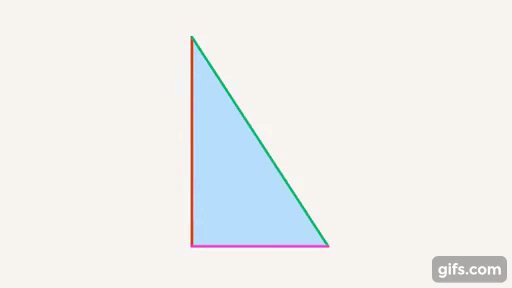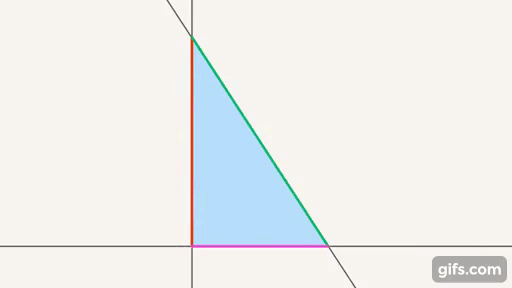
Рис. 6. Треугольник – фигура, образованная тремя отрезками прямых

Базовые геометрические фигуры – это точки, отрезки, лучи, прямые, плоскости.

Точка – это идеальный математический объект, который не имеет ни длины, ни ширины. Понятно, что если точку нарисовать, то получится далеко не точка (см. рис. 7), в лучшем случае мы можем считать, что это круг. Хотя, на самом деле, если увеличить изображение точки, оно будет иметь кривые края и т. д. (см. рис. 8). Т. е. это непонятная клякса, если подходить к этому совсем строго.

Рис. 7. Точка

Рис. 8. Увеличенное изображение точки

Для решения различных задач мы используем модели: принимаем, что есть такой объект, как точка, который не имеет ни длины, ни ширины (его размерами мы пренебрегаем). Это удобная для нас модель объекта, размеры которого не важны для решения данной задачи. Важным является ее расположение. Например, точка может обозначать начало некоторого пути.

В обычной жизни мы также пренебрегаем размерами некоторых объектов. Например, пешеход вышел из деревни. Если подробно рассматривать задачу, то возникнет вопрос: из какого места деревни он вышел? Если из дома, то какого дома? Если это неважно (пройденный путь гораздо больше, чем размеры самой деревни), мы говорим, что просто из этой деревни, то есть считаем ее точкой. Когда спортсмены соревнуются в беге на соревнованиях, то там уже важно, с какого именно места они стартуют, где у них расположены ноги и т. д. В этом примере мы не можем сказать: «Стартовал из точки». А, например, город мы можем обозначить за точку, если машина выехала из этого города и удаляется от него на большое расстояние. Точка – один из примеров таких идеальных объектов, причем важно подчеркнуть, что у него нет определения, как и у других базовых понятий.

Следующий базовый объект – это отрезок или прямая, так как отрезок – это часть прямой. Прямая – это «не кривая». Более точное определение вряд ли можно сформулировать. Луч – это, условно говоря, половина прямой, часть прямой. Отрезок – часть прямой, ограниченная с двух сторон, то есть имеющая начало и конец (см. рис. 9).

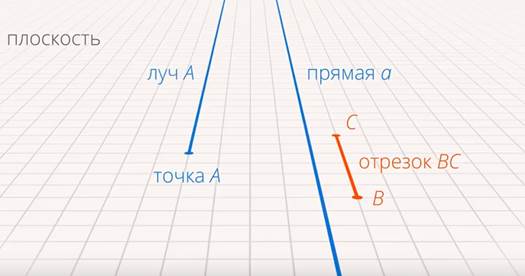
Рис. 9. Плоскость, точка, прямая, отрезок, луч

Говорят, что кратчайшее расстояние между двумя точками на плоскости – это длина отрезка прямой. Но здесь содержится тавтология, так как мы определяем прямую через кратчайшее расстояние, а кратчайшее расстояние – через прямую. Что-то из этого нужно считать определением, а что-то – интуитивно понятным. Важно, что базовые объекты определяются интуитивно (аналогично множествам в алгебре).

Следующие конструкции – это комбинации простейших объектов. Например, две прямые. Они или пересекаются на плоскости (см. рис. 11), или не пересекаются, т. е. параллельны (см. рис. 12). В жизни много примеров параллельных прямых. Например, железнодорожные рельсы (см. рис. 13).

Рис. 11. Пересекающиеся прямые

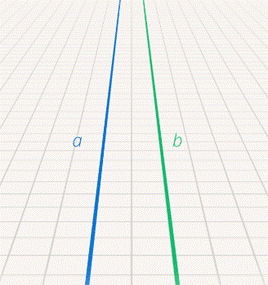
Рис. 12. Параллельные прямые

Рис. 13. Иллюстрация параллельности прямых на примере рельс

Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Т. е. мы сначала вводим объекты, а после – отношения между этими объектами.

Аналогично мы поступали с числами: ввели натуральные числа – количество предметов в множестве. А после этого изучали отношения между этими числами: дроби и т. д. (см. рис. 14).

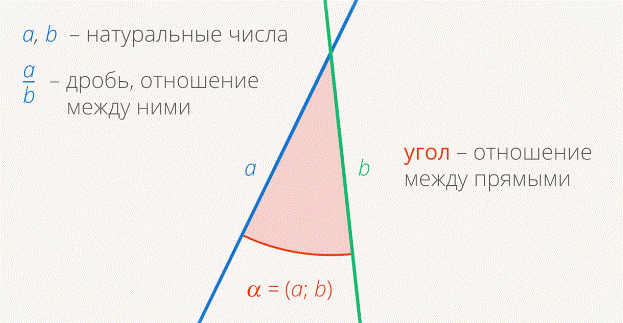
Рис. 14. Угол – отношение между прямыми

Точно так же мы изучали множества, а затем – отношения между множествами, функции.

Две прямые образуют углы (см. рис. 14). Если один из них нулевой, то прямые параллельны; если нет – прямые пересекаются. Т. е. угол – это отношение между прямыми.

Существенное отличие угла от таких отношений, как дроби и т. д., в том, что угол ограничен в своем измерении. Максимальный угол – это полный оборот (см. рис. 15). Мы его считаем равным 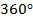. Это, конечно, условно. Мы могли бы считать полный оборот равным  или измерять в радианах – 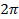. Но есть некая единица измерения угла, и она как бы ограничена. Угла большего, чем  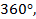на практике мы представить не можем.

Рис. 15. Максимальный угол

Можно ввести, как мы делали с отрицательными числами, новые объекты. Повернулись на один полный оборот, потом еще раз повернулись и т. д (см. рис. 16).

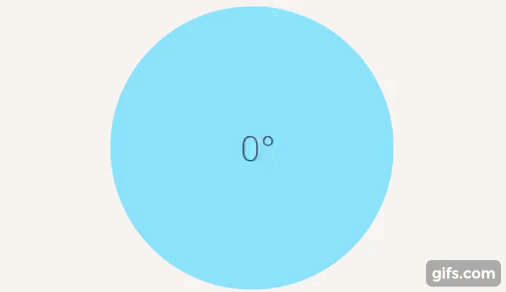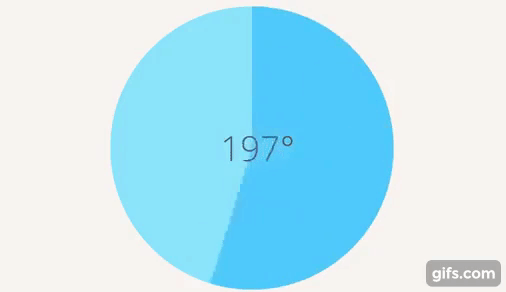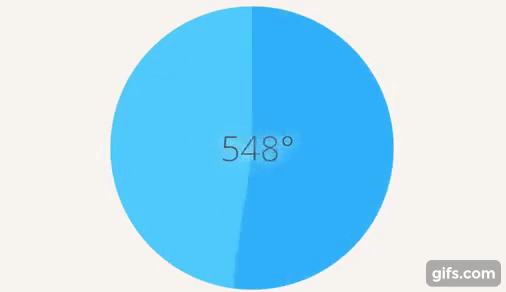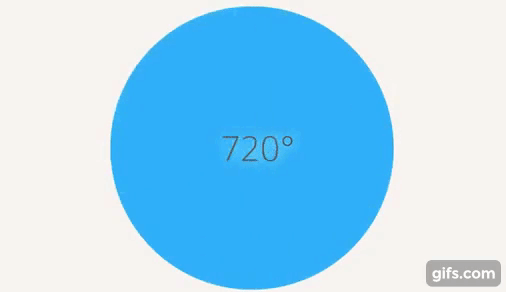
Рис. 16. Несколько полных оборотов

Мы говорили об этом в тригонометрии, когда обсуждали периодические функции. Там тоже возникает эта задача, когда мы делаем несколько оборотов и не знаем, какой именно угол, то ли 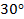, то ли 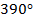,  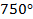и т. д (см. рис. 17).

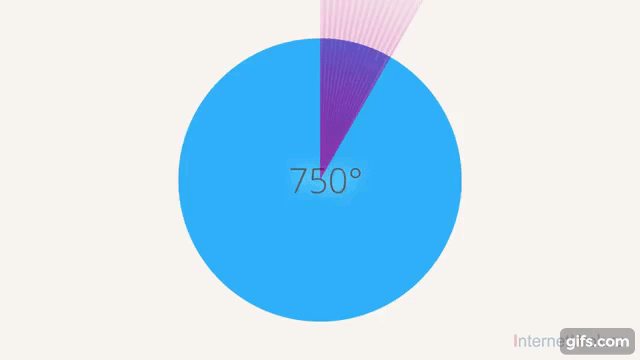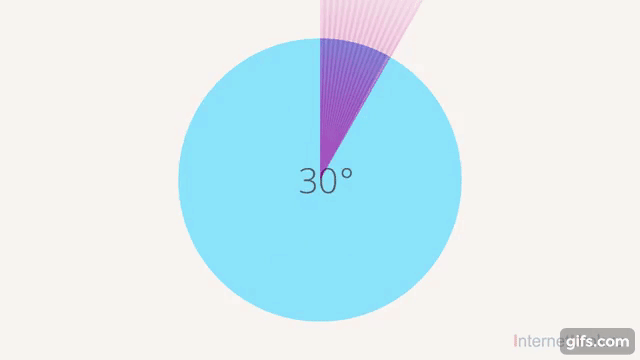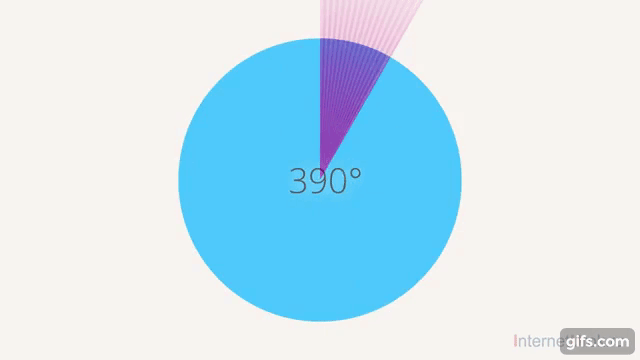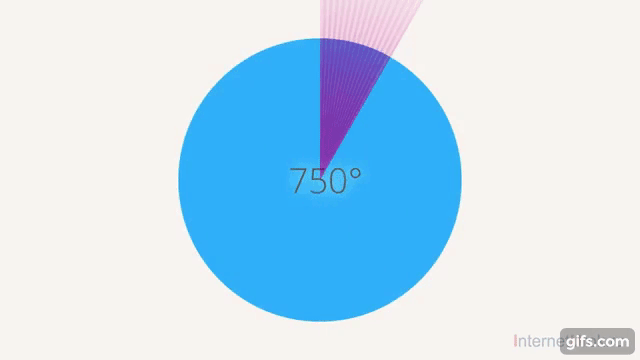
Рис. 17. Многозначность угла

Важно то, что углы можно измерять. Углов бесконечно много, так как от 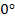 до 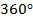 угол может принимать бесконечное множество значений. Из всего множества углов можно выделить наиболее часто встречающиеся.

Развернутый угол – угол, который образует прямая, половина от полного оборота (см. рис. 18).

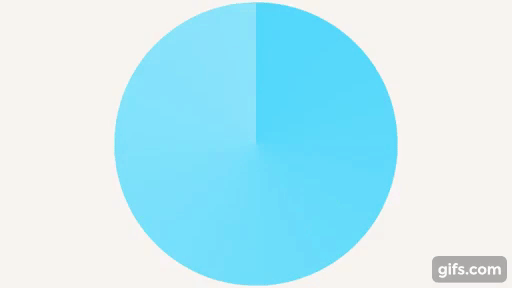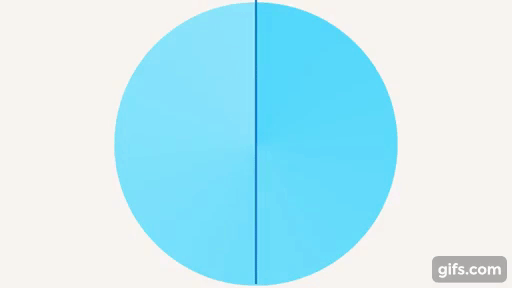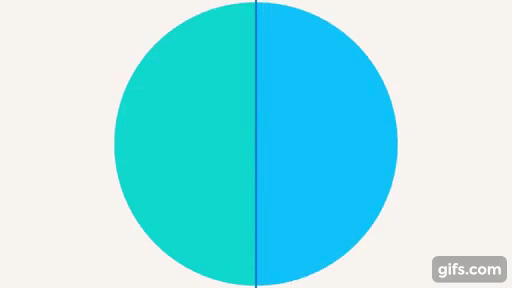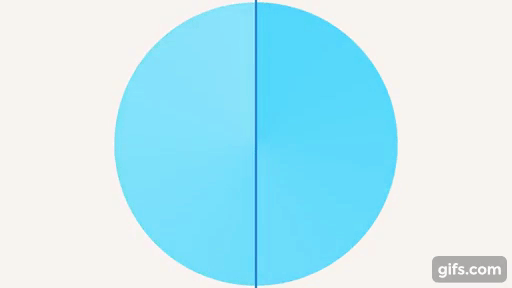
Рис. 18. Развернутый угол

При пересечении прямых может образоваться еще один особый угол – прямой (см. рис. 19).

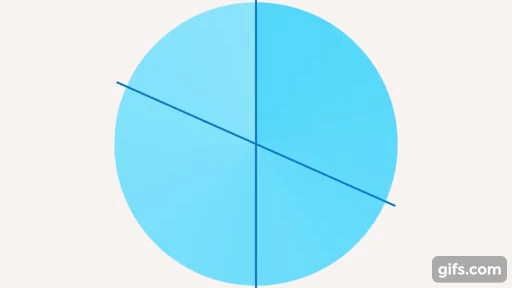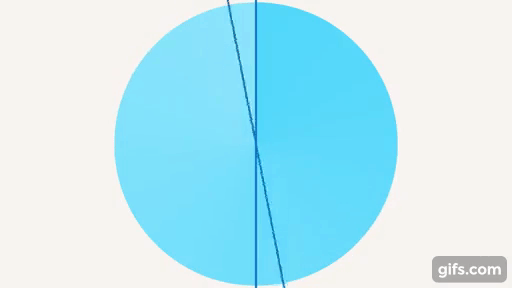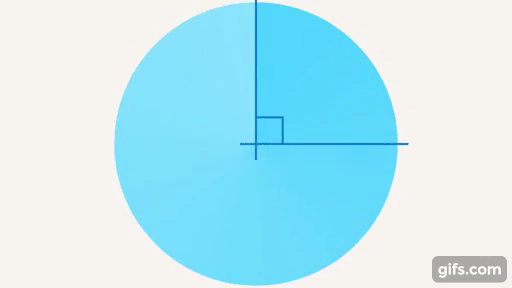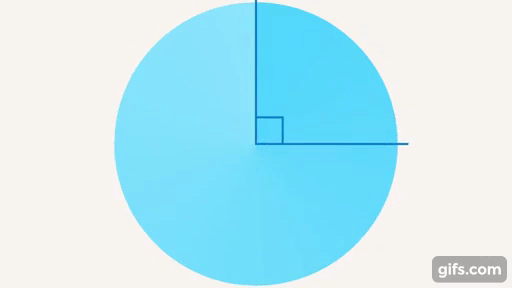
Рис. 19. Прямой угол

Замечателен он тем, что прямые, которые его образуют, расположены таким образом, что одна из них не падает ни вправо, ни влево относительно второй. Поэтому мы говорим, что стена дома должна быть расположена перпендикулярно дому, чтобы он не упал и т. д (см. рис. 20).

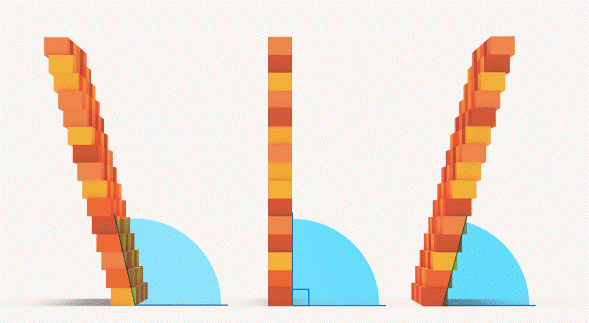
Рис. 20. Расположение стены дома, чтобы он не падал

Немного вернемся и скажем, почему мы вводим полный угол, зачем он нам и почему полный оборот равен 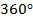. Углы можно сравнивать. Есть две прямые, то, как они связаны, – это значение угла между ними. Этот угол может быть больше, может быть меньше (см. рис. 21).

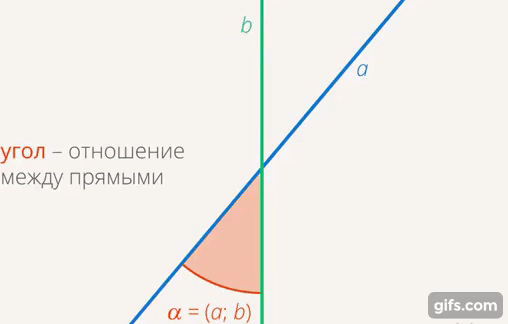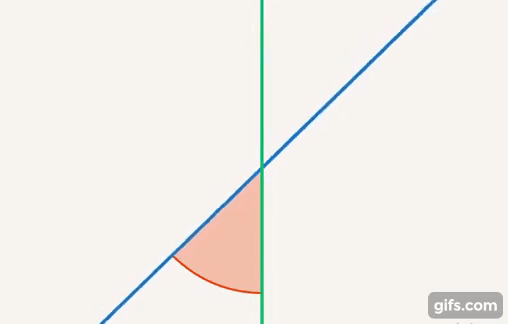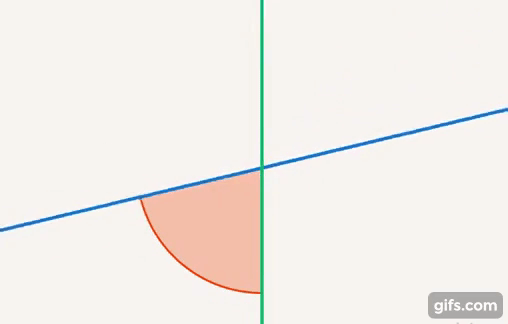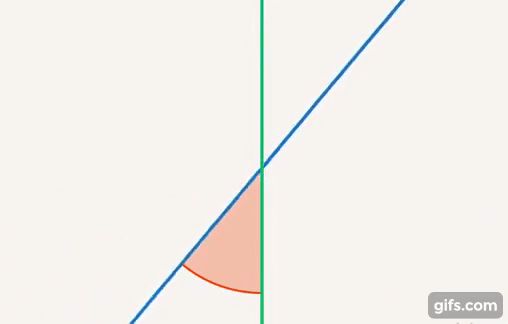
Рис. 21. Угол – отношение между прямыми

Чтобы сравнить величины, мы используем измерения. Как измерить угол? Можно взять полный круг, его за что-то обозначить и дальше выяснить, какую часть этого круга составляет этот угол (см. рис. 22).

Рис. 22. Сравнение углов

Угол, который меньше прямого, – острый угол. Больше прямого – тупой (см. рис. 23).

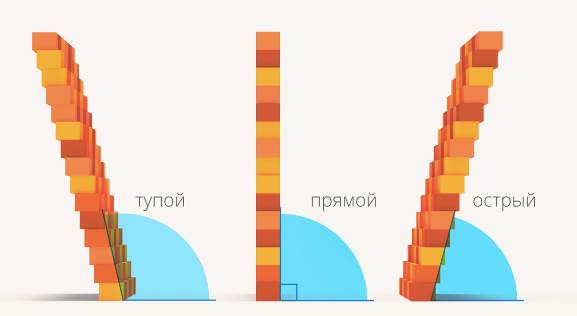
Рис. 23. Тупой, прямой и острый углы

Дальше мы будем использовать угол, то есть отношение между прямыми, в других фигурах, таких как треугольники и т. д. Сейчас мы знаем, что, если у нас есть две прямые, мы можем ввести отношение, которое называется углом, и, соответственно, сделать некую классификацию. Выделены два угла: один нулевой – его образуют параллельные прямые; прямой угол – образуют перпендикулярные прямые (когда все 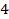 угла, образующихся при пересечении двух прямых, равны (см. рис. 24)).

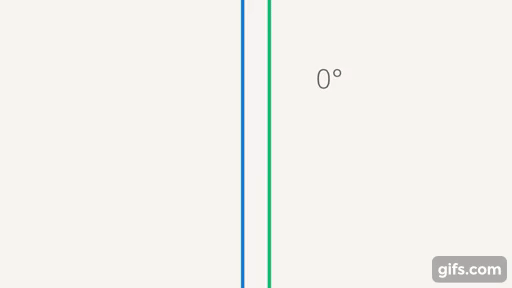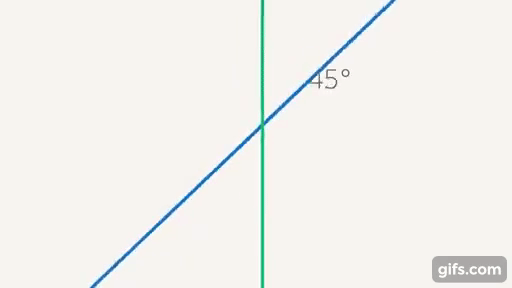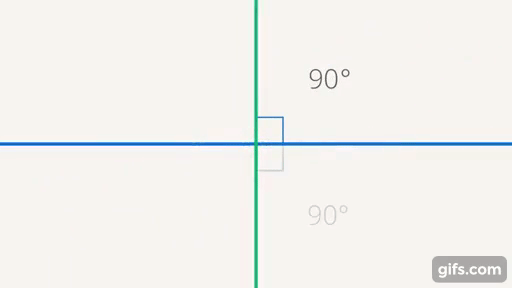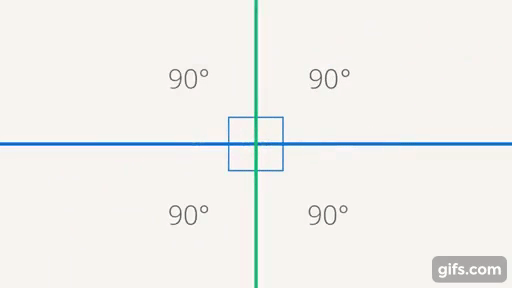
Рис. 24. Параллельные и перпендикулярные прямые

1-й случай: все три прямые параллельны (см. рис. 25).

Рис. 25. Параллельные прямые

2-й случай: две прямые параллельны, а третья их пересекает (см. рис. 26).

Рис. 26. Две прямые параллельны, а третья их пересекает

Рассмотрим такой пример: один человек с закрытыми глазами проводит прямую карандашом, а другой после этого произвольно поворачивает лист – в результате после трех таких операций получится треугольник. Или, например, если с закрытыми глазами бросить три спички на бумагу и продолжить их, то также получится треугольник (см. рис. 27).

Рис. 27. Получение треугольника

Вывод: три прямые, проведенные на плоскости случайным образом, с вероятностью 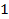 образуют треугольник (все остальные предельные случаи – три прямые параллельны, пересекаются в одной точке, две прямые параллельны, а третья их пересекает – вероятны так же, как и выпадение монеты на ребро). Поэтому эту фигуру мы так подробно и изучаем в школе.

С одной стороны, треугольник образуют три прямые. Посмотрим на треугольник с другой стороны, т. е. как на фигуру, состоящую из отрезков. Про два отрезка ничего нельзя сказать, они не могут замкнуться, так как всегда есть начало, есть конец, и они не совпадают (см. рис. 28).

Рис. 28. Два отрезка

Если добавить третий отрезок, то получим наименьшую возможную замкнутую ломаную – треугольник (см. рис. 29).

Рис. 29. Наименьшая замкнутая ломаная – треугольник

Исходя из этих свойств и особенностей, из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников, и т. д. (см. рис. 30).

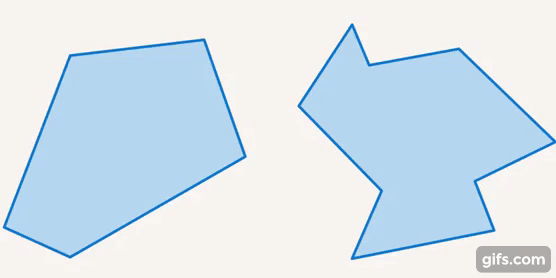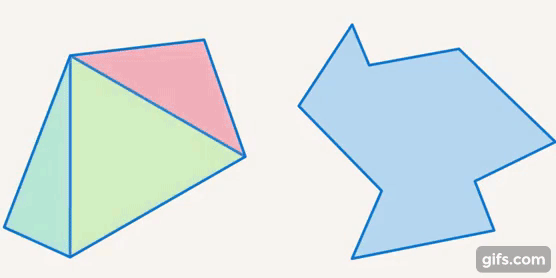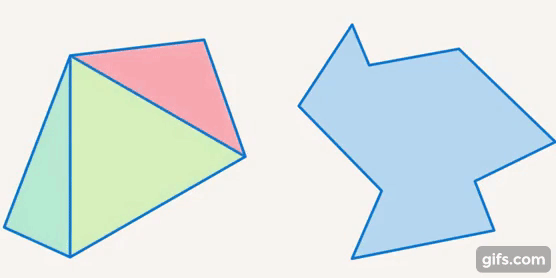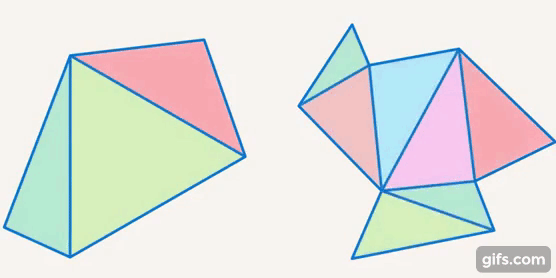
Рис. 30. Многоугольники состоят из треугольников

Треугольники изучаются потому, что на практике имеют большое значение. Для того чтобы построить устойчивую фигуру, нужно использовать треугольники. Например, вантовый мост (см. рис. 31). Несущие конструкции состоят как раз из треугольников.

Рис. 31. Вантовый мост

Треугольник также используется для измерения расстояний (см. рис. 32), а также изучаются его взаимоотношения с окружностью, которая тоже является элементарной конструкцией (см. рис. 33).

Рис. 32. Измерение расстояний с помощ

Объемные фигуры из картона выкройки. Геометрические фигуры из бумаги своими руками с описанием и фото схем

Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.

Как сделать объемные геометрические фигуры

Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.

Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.

Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.

Из бумаги

Из картона

Развертки куба

Треугольника

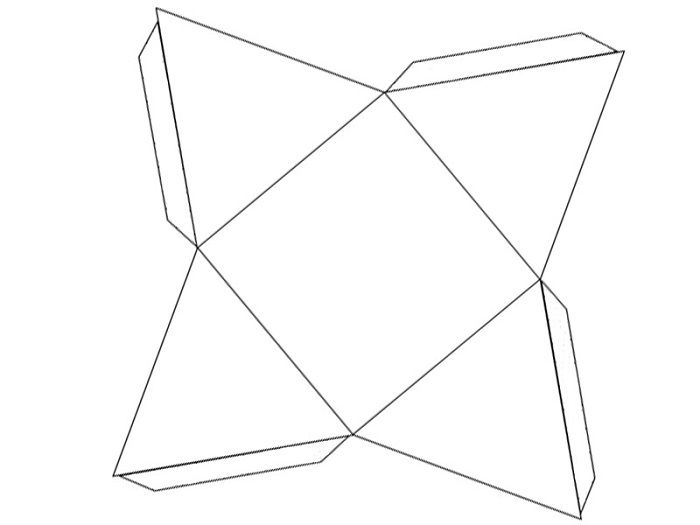
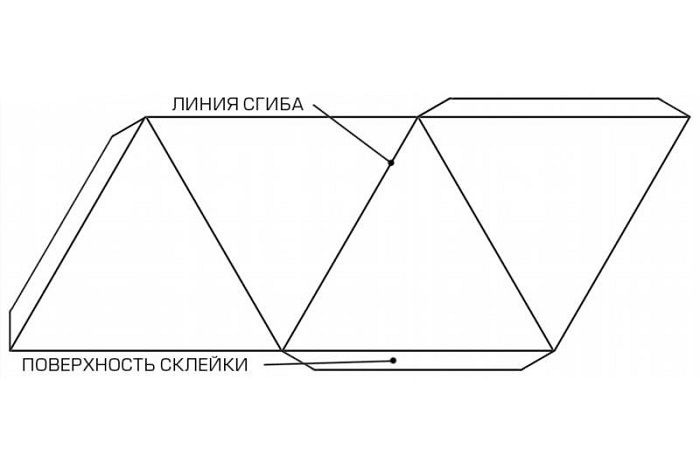
Прямоугольника

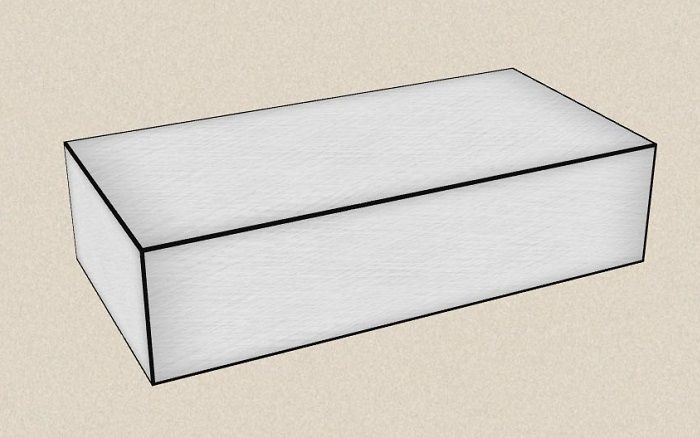
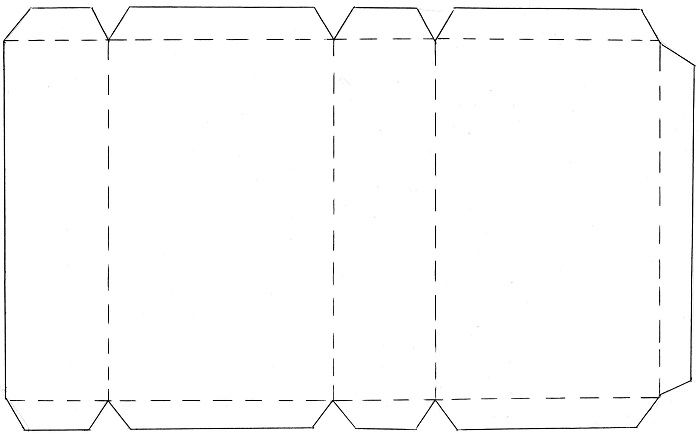
Цилиндра

Ромба

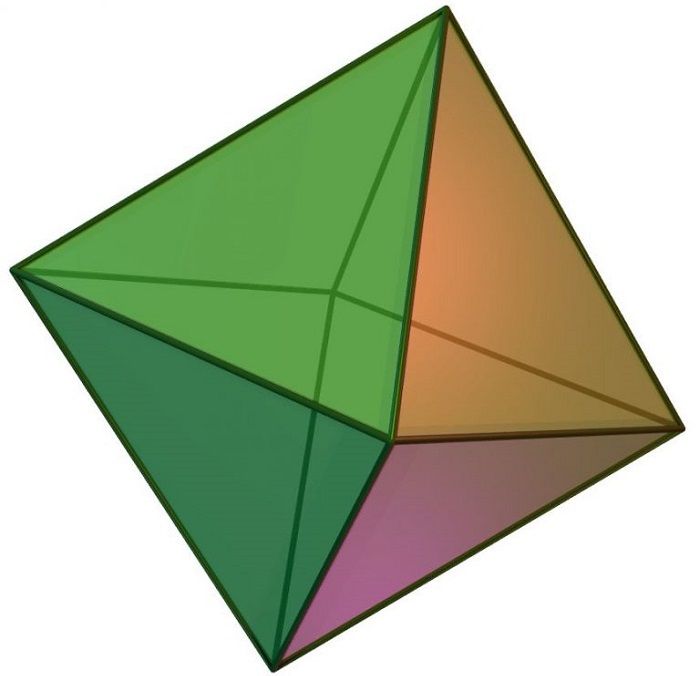
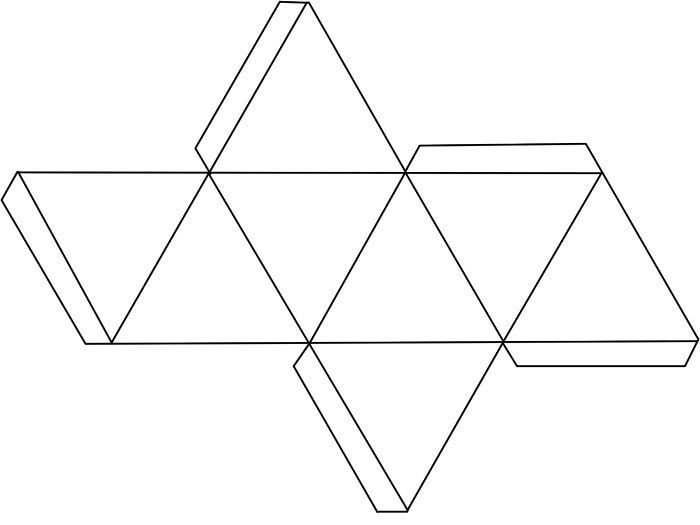
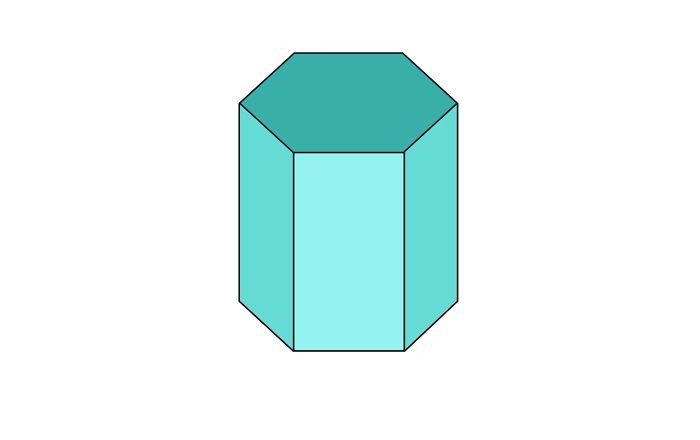
Призмы

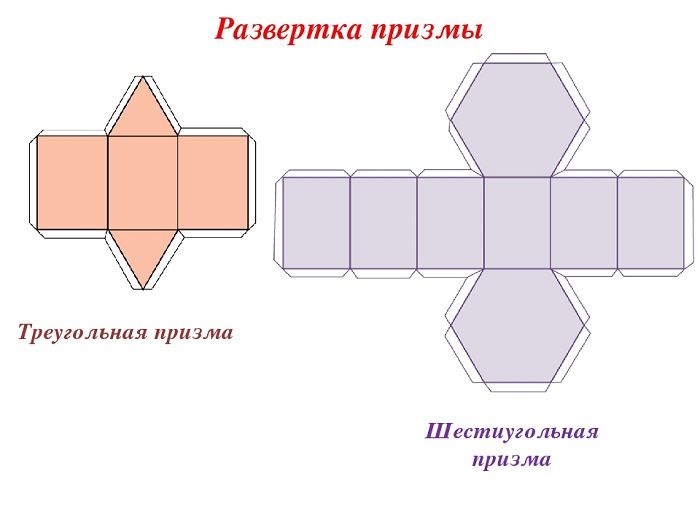
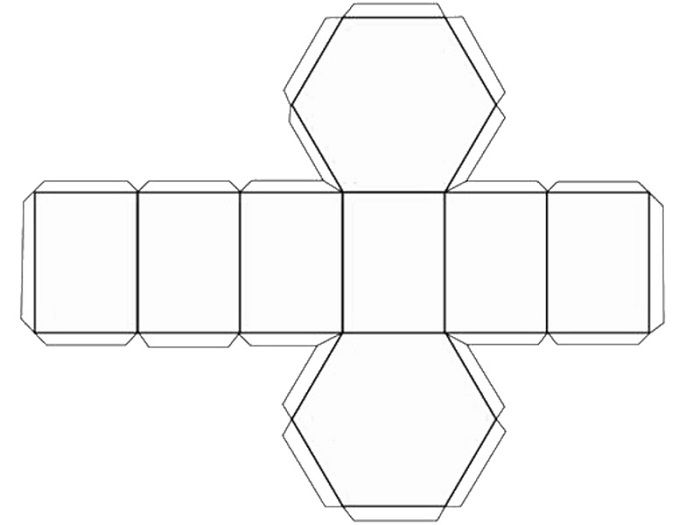
Схемы для вырезания

Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.

Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).

Конуса

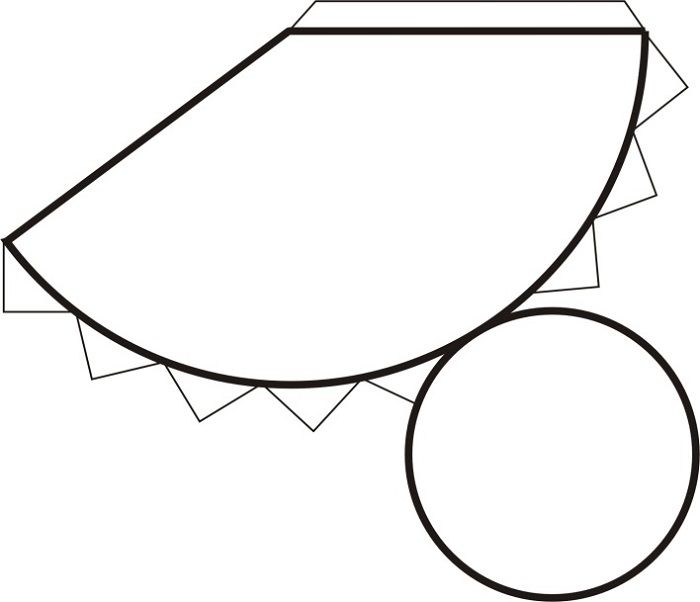
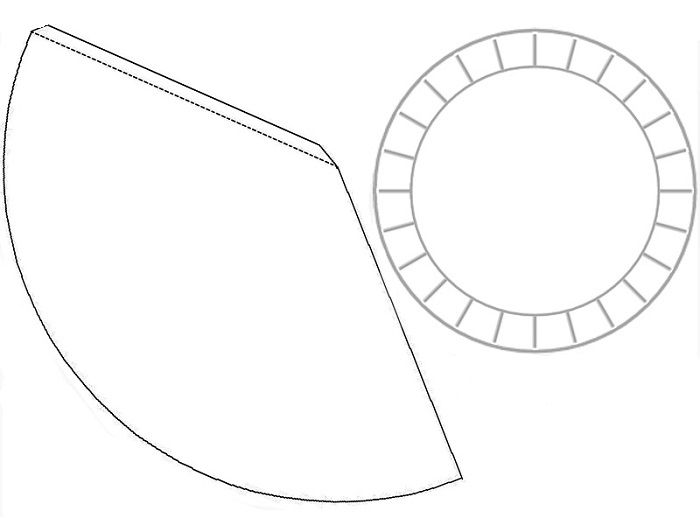
Пирамиды

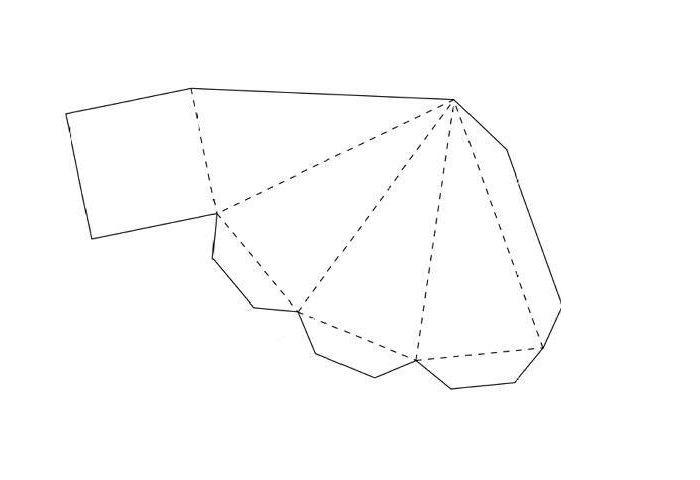
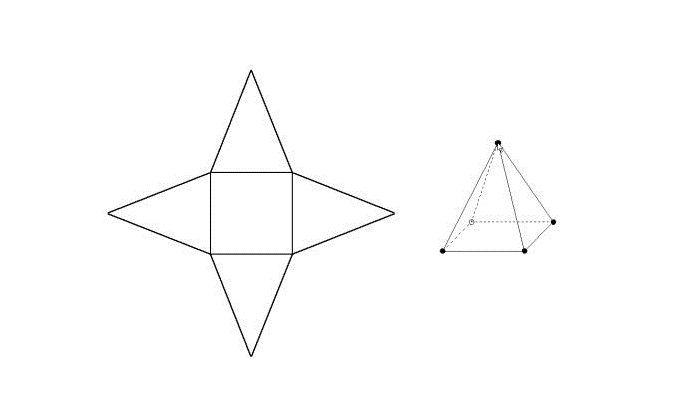
Шестигранника

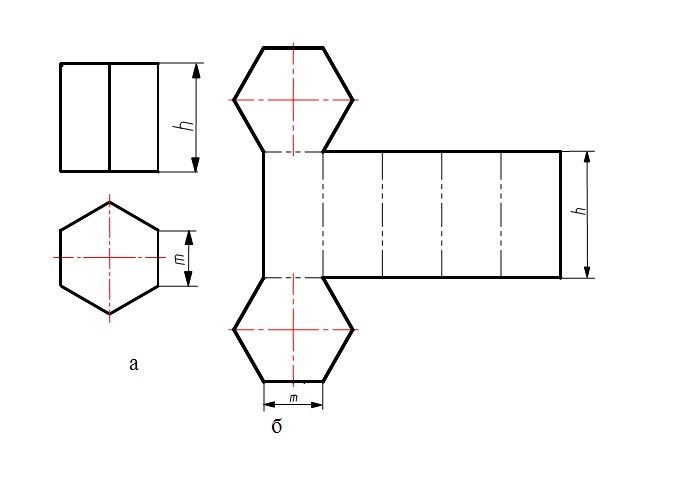
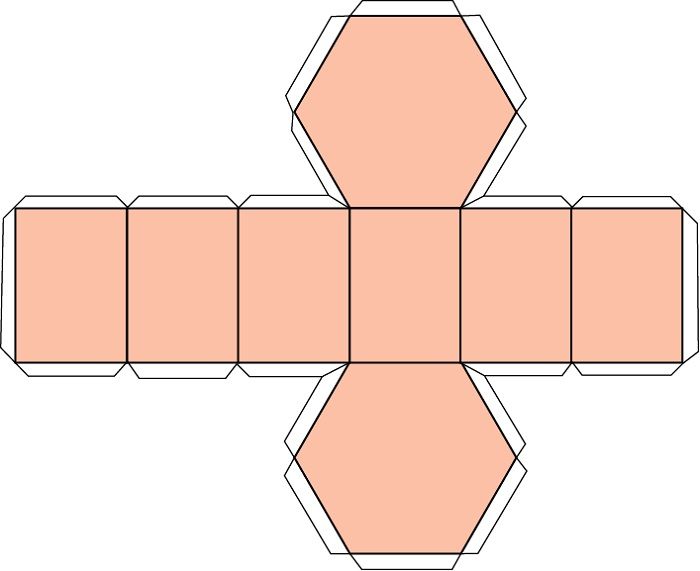
Макета с припусками

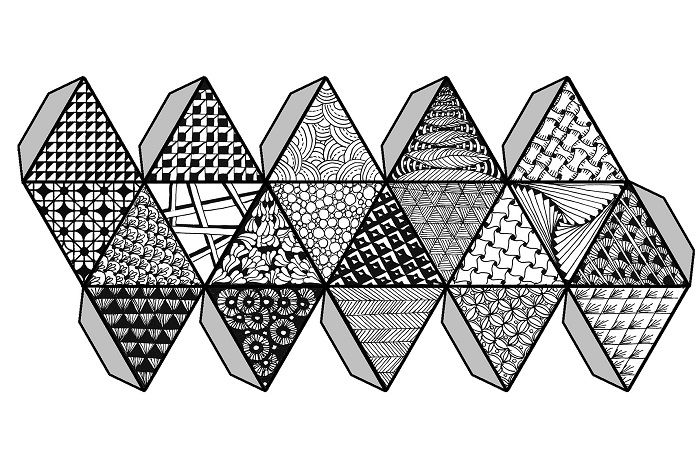
Параллелепипеда

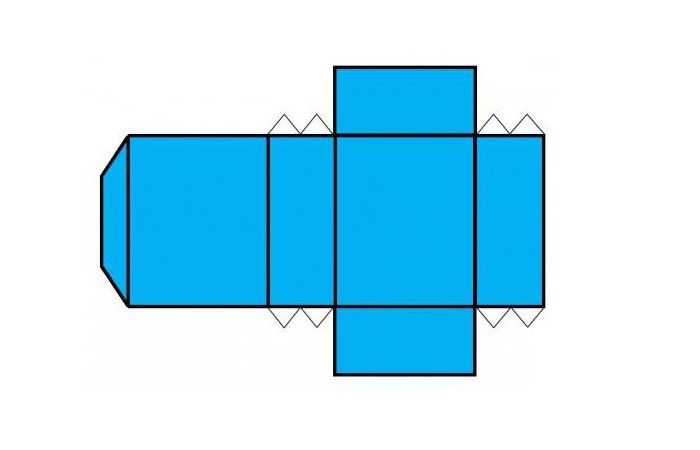
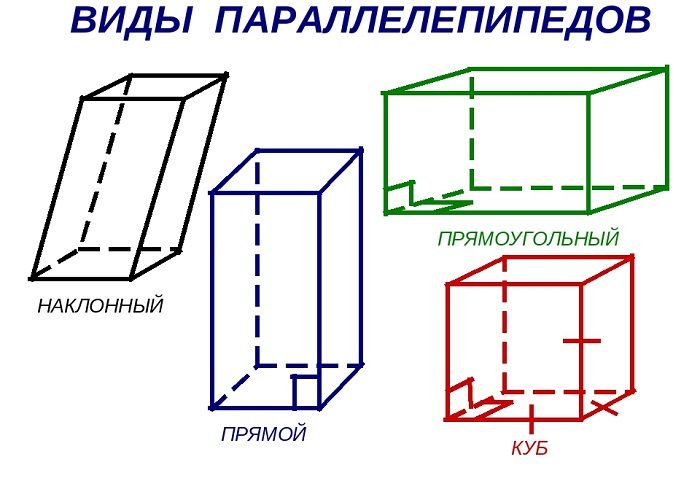
Трапеции

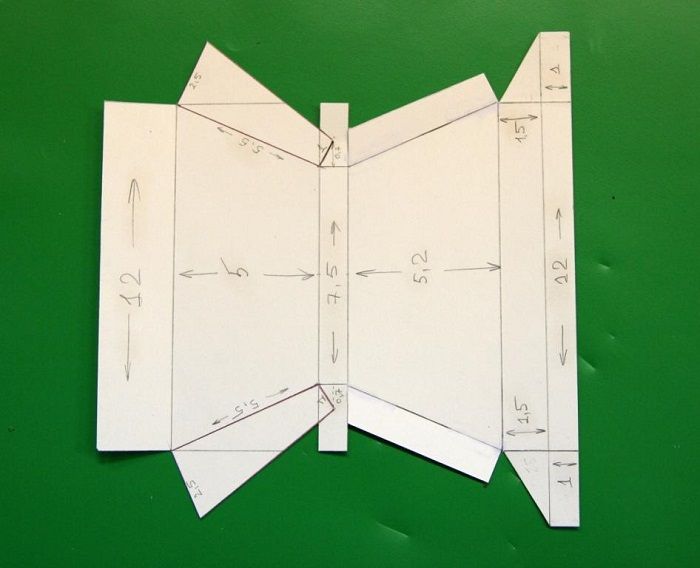
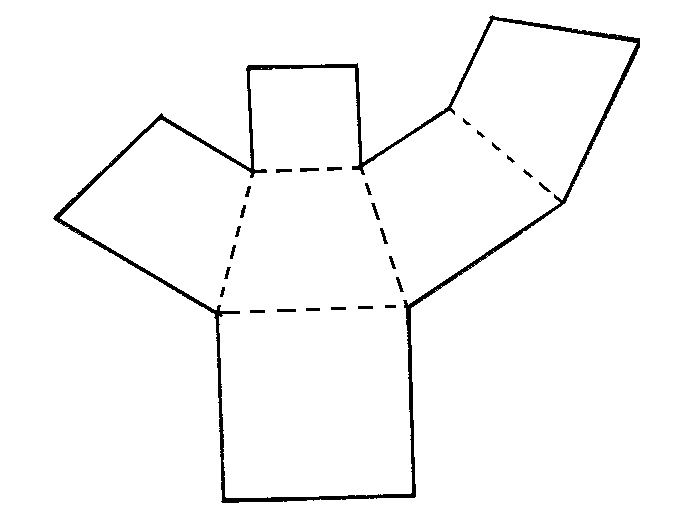
Овала

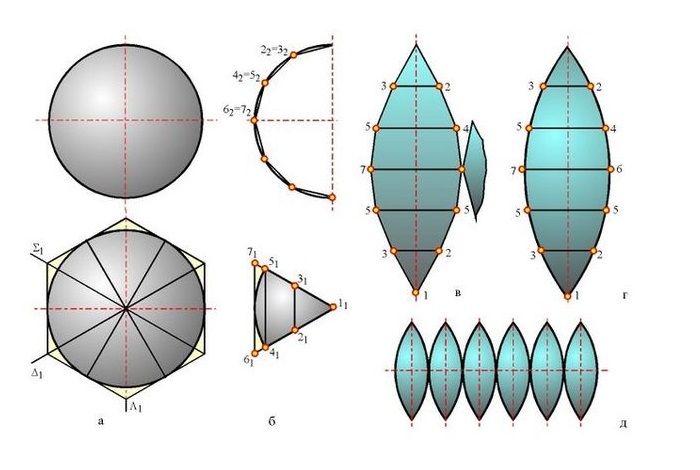
Шара

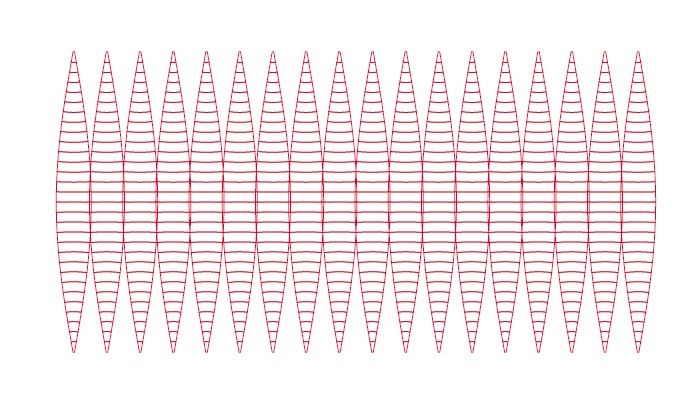
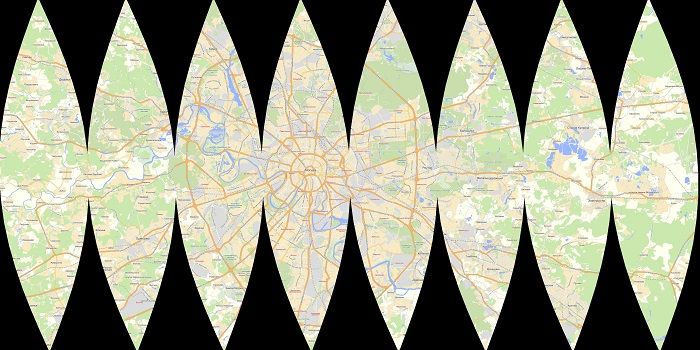
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.

Материал, из чего можно сделать плотный шар — картон или плотная бумага.

Многогранника

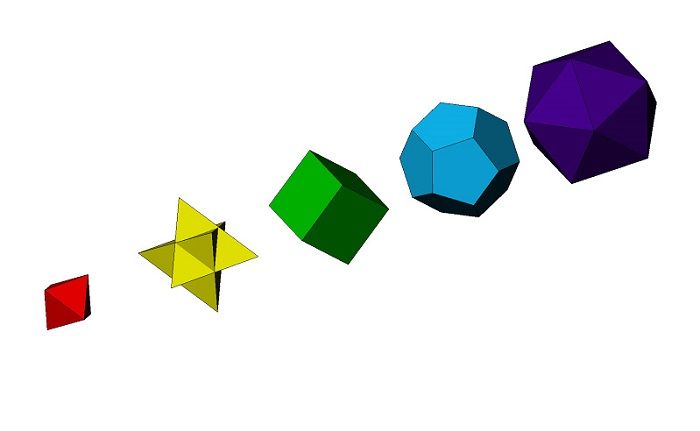
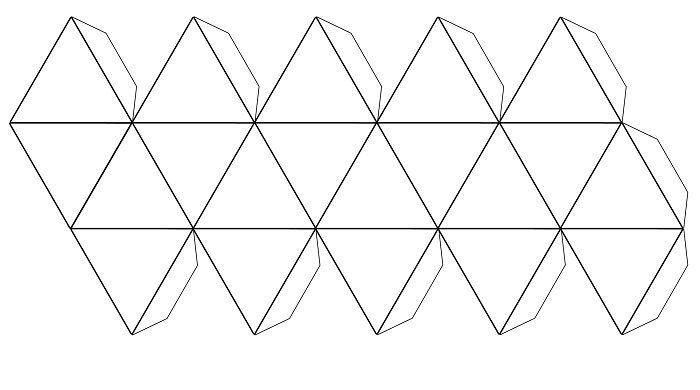
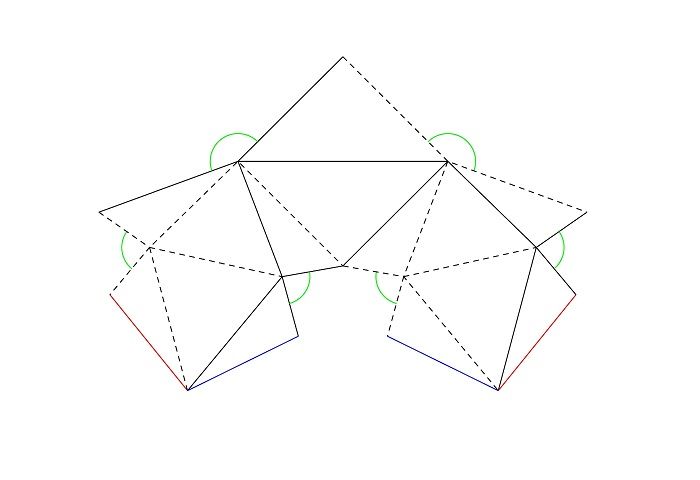
Параллелограмма

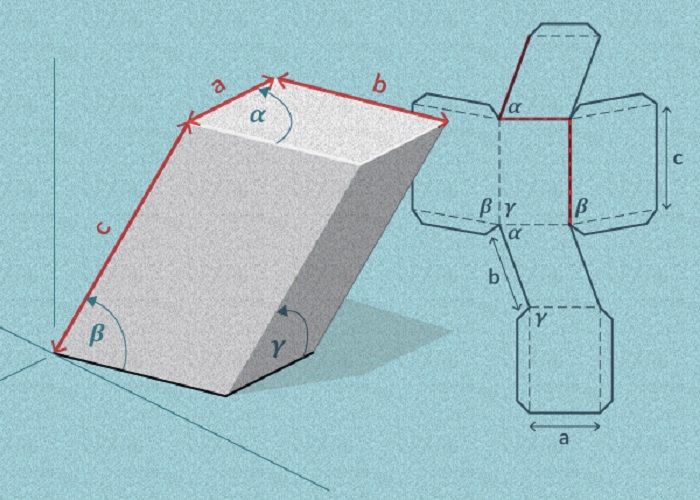
Шаблоны для склеивания

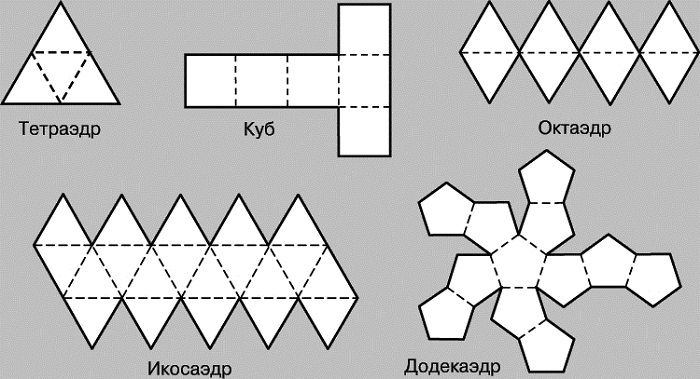
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.

Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.

Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.

Сложных фигур

Деление окружности, или Геометрия для чайников

Приветствую всех мастеров и мастериц!

Очень многие из нас, учась в школе, думали, что очень многие предметы школьной программы в жизни нам никогда не понадобятся. Я так думала про геометрию. Однако жизнь сложилась так, что именно геометрия мне оказалась и нужна.

Одной из основных сложностей при создании круглого орнаменты является его симметричность. Иногда хочется, чтобу у нас был точный 8-ми гранник, иногда 5-ти конечная звезда, а иногда нужен 7-ми конечный цветок.

Эту глобальную проблему симметричного деления окружности на равное количество частей можно решить просто при помощи циркуля, линейки, листа бумаги и геометрии.

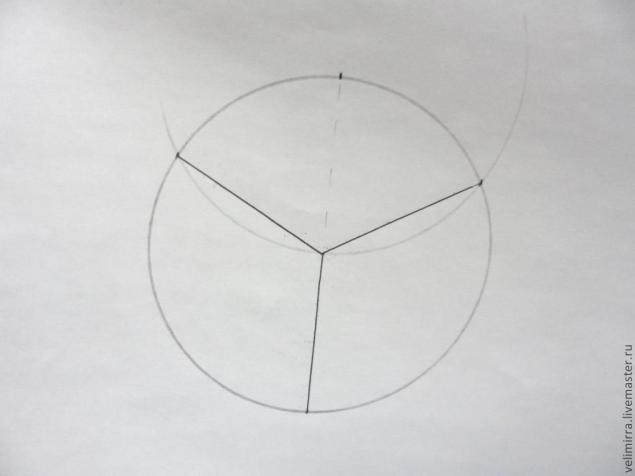
Деление окружности на 3 равных сектора.

Для начала нам понадобиться сама окружность. Рисуем ее при помощи циркуля

Выбираем на поверхности окружности любую точку, отмечаем ее карандашиком. Далее циркулем отмеряем радиус нашей окружности (кто забыл — это расстояние от центра окружности до любой ее точки)

Ставим наш циркуль с набранным радиусом в точку, которую мы на окружности отметили и проводим дугу до пересечения с нашей основной окружностью.

Через точку на окружности и центр окружность проводим линию до пересечения с гранью.

Таким образом мы получили 3 точки на нашей окружности.

Теперь из центра проводим линии, соединяя центр с этими точками и у нас образовались 3 одинаковых сектора.

Деление окружности на 4 равных сектора.

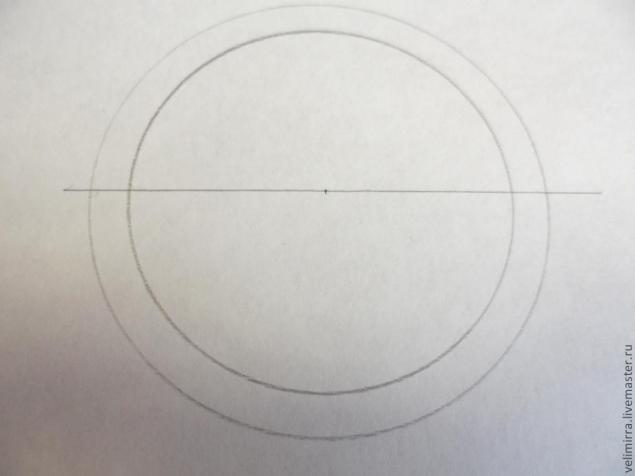
Начинаем опять с окружности, необходимого нам диаметра. Назову ее окружность 1.

Через центр окружности 1 проводим линию до пересечения с обеими сторонами окружности 1.

Из центра окружность 1 при помощи циркуля рисуем окружность больше диаметра — окружность 2.

Ставим ножку циркуля в точку на пересечении наше прямой линии и окружности 2 и из нее проводим дугу. Расстояние от точки на окружности до дуги равно диаметру окружности 1. (диаметр = 2 радиусам). Ту же процедуру повторяем с точкой на другой стороны окружности.

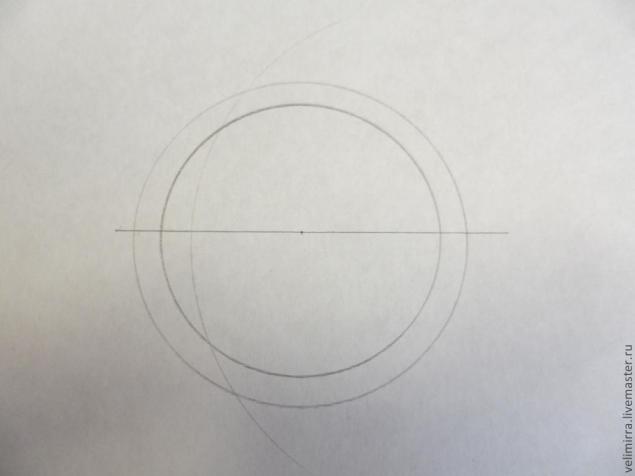
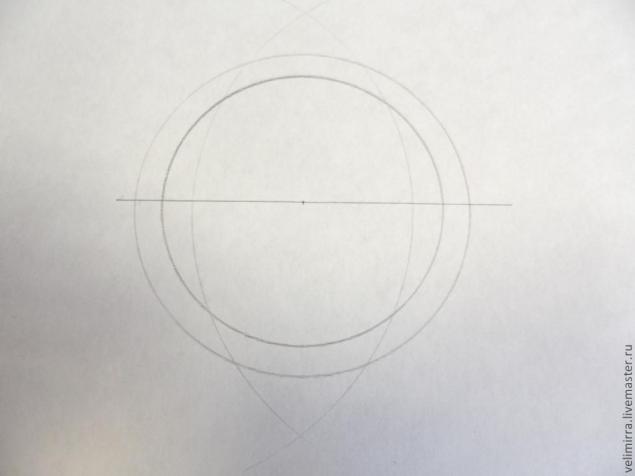
У нас есть 2 новые точки, появившиеся на пересечении дуг. Соединяем их и получаем окружность, разбитую на 4 ровных сектора.

Деление окружности на 5 равных секторов.

Начало работы с делением окружности на 5 частей очень схожа с делением окружности на 4 части, поэтому я начну уже с разделенного круга на 4 части.

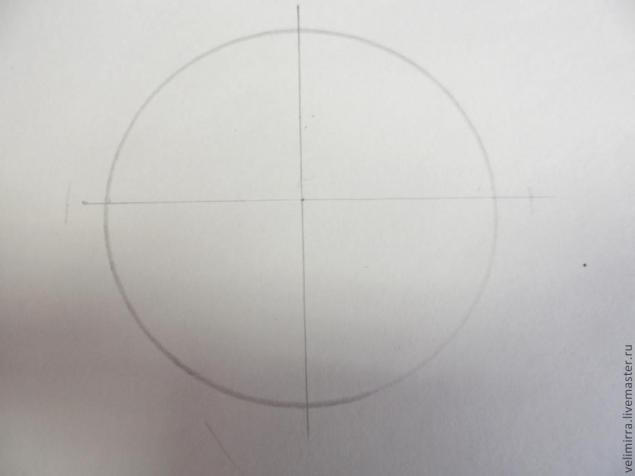
Циркулем набираем радиус нашей окружности и ставим ножку в одну из имеющихся у нас точек. В моем случае это левая точка. Проводим дугу до пересечения ее с основной линии окружности.

Соединяем получившиеся точки при помощи линейки и находим новую точку пересечения (точка Н)

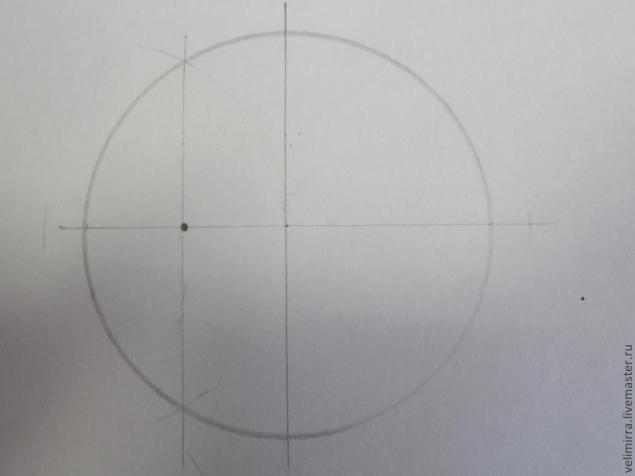
Циркулем набираем расстояние от верхний точки на окружности до точки Н. Ставим ножку в точку Н и проводим дугу и получаем еще одну точку (точка М)

Ставим ножку циркуля в верхнюю точку окружности и набираем расстояние до точки М.

Ставим ножку циркуля в верхнюю точку и откладываем набранное нами расстояние на нашей окружности.

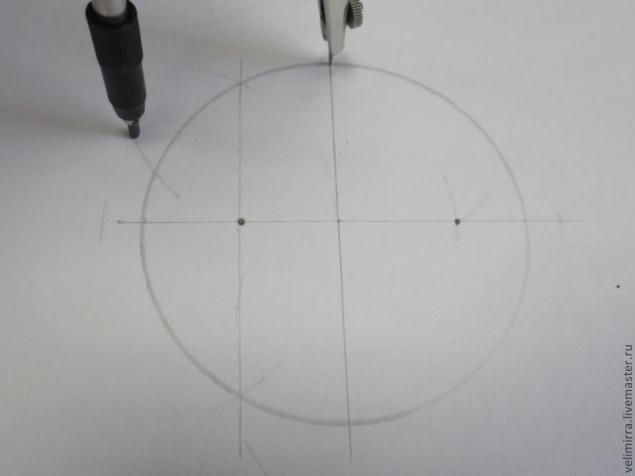
Ставим циркуль в получившуюся точку и еще раз откладываем это расстояние. Таким же образом ставим еще 2 точки.

У нас получилось 4 отложенных точки и 1 верхняя точка окружности. Соединяем центр окружности с этими точками и получаем 5 равных секторов.

Деление окружности на 6 равных секторов.

Нам снова нужна окружность.

Берем любую точку на этой окружности, ставим в нее ножку циркуля с набранным расстоянием радиуса и проводим дугу до пересечения с нашей окружностью.

Далее соединяем выбранную нами точку с центром окружности и находим еще одну точку с противоположной стороны.

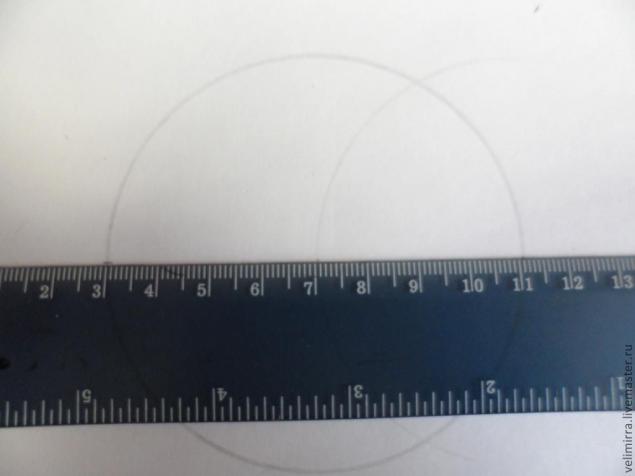
Из этой точки таким же расстоянием проводим еще одну дугу.

Мы получили 6 точек — 2 мы шали при помощи дуг, 1- наша выбранная и 1 найденная при помощи линейки. Соединяем их с центром и получаем 6 равных секторов.

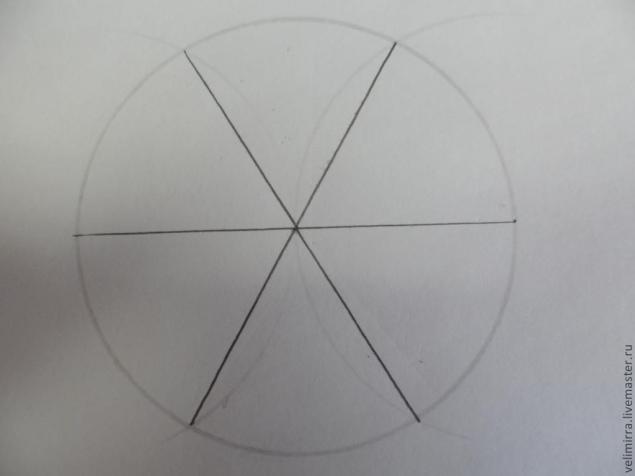
Деление окружности на 7 равных секторов.

Чтобы не повторяться и не описывать уже знакомые алгоритмы, берем за основу момент нахождения точки Н для разбития окружности на 5 частей.

Отмеряем циркулем расстояние от точки Н до точки на окружности.

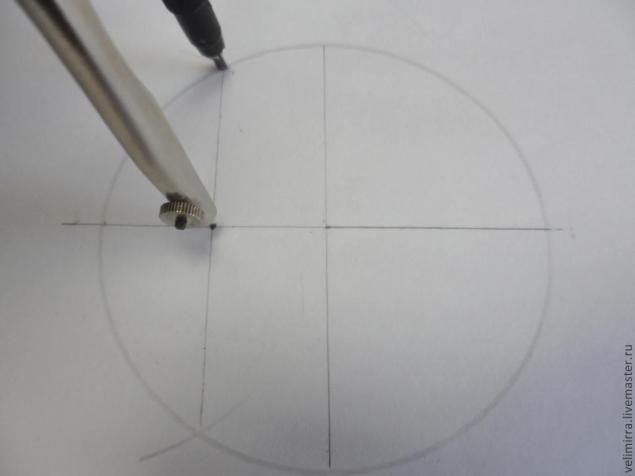
Ставим ножку циркуля в верхнюю точку и набранным на циркуле расстоянием откладываем точки, аналогично как мы делали в случае разбивки окружности на 5 частей

Соединяем наши новые точки с центром и получаем 7 равных секторов.

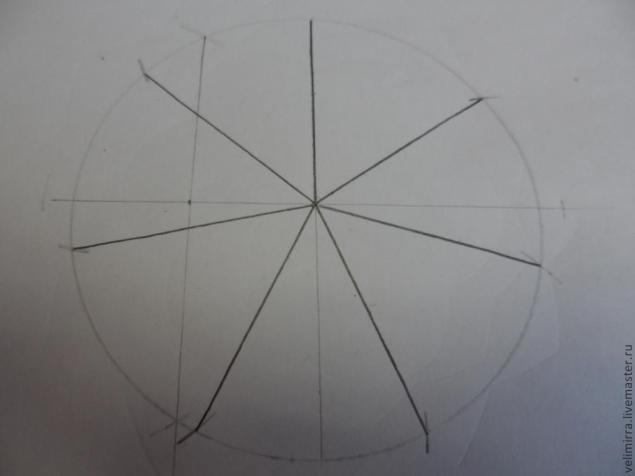
Используя эти простые приемы можно создавать геометрические орнаменты различной сложности

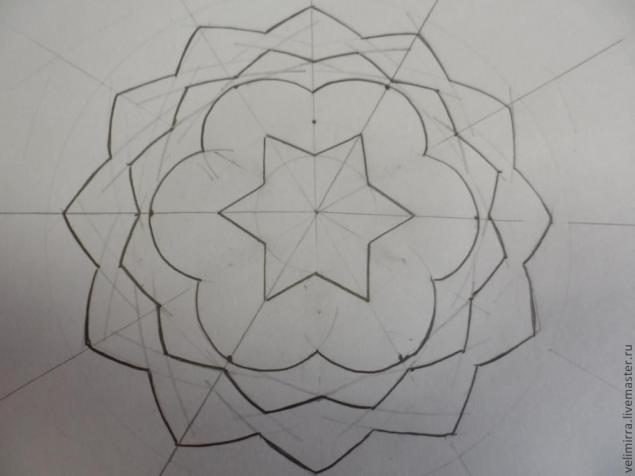
Надеюсь мой МК окажется кому-то полезным.

Удачи в создании шедеворов.

Ваша Velimira

Как решать задачи по геометрии. Часть 1

Геометрическая логика при решении задач

Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.

Это про тебя? Тогда ты попал туда, куда нужно!

Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.

Сразу оговорюсь — без знания теории в геометрии никак. В смысле, вообще никак, от слова «совсем». Чтоб тебе было полегче при чтении этой статьи, я буду внутри решений задач в скобках курсивом указывать используемые свойства и теоремы. Но помни: если вдруг в знании теории у тебя пробел – закрытие его за тобой! Бери учебник и читай. Причем главные вещи – заучивай (или понимай). Знать теорию – обязательно!

Ладно, к делу.

Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать? Как достичь цели?

Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.

Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.

К чему весь этот разговор? Решение задачи по геометрии это точно такой же «квест», только математический . Вдумайся: у нас всегда есть некоторые исходные данные и есть то, что нужно найти (или доказать – разницы на самом деле практически нет). И наша задача – построить логическую цепочку от исходных данных к цели. Строительным материалом при этом у нас будут данные (исходные и полученные при рассуждениях), а также теоремы и свойства.

Ладно, давай уже конкретный пример разберем.

Задача. В треугольнике \(ABC\) из точки \(B\) проведена высота \(BH\). Найти длину отрезка \(AH\), если известно, что сторона \(AC\; =\; 14\) см и угол \(A\) равен углу \(C\).

Так. С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.

В геометрии это означает:

1. построить чертежа выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
2. выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
   

Хорошо. Значит, текущая ситуация у нас такова:

Давайте потихоньку развеивать туман. Нам известно, что углы \(А\) и \(С\) равны, а это значит, что треугольник \(АВС\) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.

Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что \(BH\) – высота. А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.

А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны). Но тогда получается, что точка \(H\) делит сторону \(AC\) пополам. То есть \(AH = HC\).

Стоп. Так у нас же есть длина стороны \(AC\)! И если мы знаем, что точка \(H\) делит сторону \(AC\) пополам, значит, \(AH\) равен половине \(AC\)! Таким образом, получаем, что \(AH = AC/2 = 14/2=7\) см.

Готово. Ответ получен.

Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове. А записывается примерно так:

Как проверить геометрию комнаты своими руками: полы и стены

Часто в вашей квартире нет правильной геометрии помещения. Это встречается сплошь и рядом и порой ничего страшного не представляет. Обязательные углы в 90 гр. по всей квартире — это миф. То же касается и вертикали стен — отклонения по нормам СНиП не должны превышать 15 мм от вертикали по высоте стены.

Что же касается пола, то от неразрывно связан с длиной стен и углами. В общем, если ваше помещение не представляет собой ровный прямоугольник — это не беда, у всех так. Давайте посмотрим как проверить геометрию помещения, определить отклонения углов от 90 градусов и стен от вертикали и узнаем как это можно исправить и нужно-ли вообще исправлять.

Замеряем длину стен и рисуем план

Попробуем определить геометрию нашего помещения своими руками и замерим длину стен, начертив на бумаге схему с указанием размеров.

Рисуем план на бумаге, лучше миллиметровой

Что дал нам такой план? Размеры сторон нашего прямоугольник, которые могут отличаться. Две «параллельные» стены, оказываются не параллельны и имеют разный размер, соответственно углы у нас уже не могут быть прямыми и получается, что геометрия нарушена.

Небольшие отклонения в длине стен — это в целом не страшно, если 0,5-1 см на всю площадь. Гораздо хуже, если больше — 2-3 см. Чем это грозит? Грозит некоторыми не очень приятными последствиями. Во-первых углы будут не 90 градусов. «И что?» — спросите вы. Иногда ничего, и по большому счёту везде в квартирах углы не строго 90 градусов.

Если это комната, то может быть так, что установив в угол шкаф, и прислонив его вплотную к одной из стен, вы поймёте, что между второй стеной и стенкой шкафа образовался зазор. Тоже касается и вертикальности стен, но об этом чуть далее. Углы строго 90 градусов в квартире (+/- 1-2 гр.) по большому счёту нужны лишь на кухне, в тому углу, где вы вешаете кухонную мебель.

Из-за не строгой геометрии помещения могут быть зазоры между стенами и мебелью

Второе место, где крайне желательна строгая геометрия помещения — это ванная комната, а именно то место, где установлена ванная (или душевая кабина, но ванная в особенности).

Возможная геометрия ванной комнаты

Часто геометрия несущих стен очень даже не плохая, иногда нюансы кроются в перегородках. Вот у них геометрия может быть «не очень».

Что нужно сделать? Обязательно проверьте:

1. Углы, к которым будет примыкать ванная.
2. Угол, где будет размещена кухонная мебель.

Всё остальное не столь важно и в бюджетных ремонтах углы под 90 градусов везде не выводятся, да и в дорогих часто тоже оставляют как есть. Проверить можно с помощью угольника, можно приобрести в магазине, или чем-то, у чего угол заведомо 90 градусов (да хоть квадратной табуреткой).

Что делать, если геометрия помещения нарушена и чем это грозит?

Если геометрия помещения нарушена и угол в нужных местах не 90 градусов, отклонения значительные, порядка 1-2 см на метр, то нужно выравнивать. Это называется штукатурные работы. О выравнивании углов будет написана отдельная статья (тут поставить ссылку — прим.), а далее мы поговорим чем ещё может грозить неправильная геометрия.

Покрытие пола будет уложено не ровно — это встречается сплошь и рядом, и ничего страшного собой не представляет, главное попробовать «затолкать» подрезки под мебель или в места, где они будут наименее заметны.

Укладка ламината в помещении с не правильной геометрией

На рисунке выше видно что ламинат будет уложен с подрезками, они могут быть больше или меньше, но с 2—х сторон разного размера. Это сплошь и рядом, когда геометрия помещения не выравнивается. Тоже касается и напольной кафельной плитки. Что бы такого избежать, нужно выравнивать геометрию, а это большие затраты и работа профессионала.

С углами вроде разобрались, определились, что угол 90 градусов обязателен лишь в двух местах: на кухне, где будут стоять/висеть шкафы и в ванной комнате, где будет стоять ванна.

Теперь посмотрим на вертикальность стен, это тоже важно и опять же особенно важно в тех же двух местах: в ванной комнате (теперь уже во всей) и на кухне, на 2-х смежных стенах со шкафами. Другие места по желанию, но в бюджетном ремонте вертикаль стен везде не выводится.

Определяем вертикальность стен и углов

Берём:

• отвес,
• либо длинное (2 м) правило с пузырьковым уровнем,
• либо пузырьковый уровень меньшей длины (от 30 см) и ровную длинную рейку или правило без уровня, к которой прислоним уровень.

Самое дешёвое — отвес, попробуем работать им. Его даже своими руками можно сделать, взяв капроновую нить и привязав к ней с одного конца грузик, скажем гайку, грамм на 100, а лучше на 200.

Отматываем верёвку в длину потолка, грузик болтается снизу, до пола не достаёт. Далее прислоняем верхний край нити к стене и смотрим на грузик…

Стена может быть завалена как в одну сторону, так и в другую

Так проходим по углам и по центру стены. Удобнее, конечно, замерять правилом с пузырьковым уровнем. Если отклонения не превышают 15 мм (это по СНиП), то всё в порядке. Если больше, опять же нужно выравнивать, НО необходимо только на кухне и в ванной комнате. Там желательно, что бы вообще отклонений не было.

В ванной будет уложена плитка или панели, ну или вы вообще ошпаклюете и покрасите стены, по-этому тут тоже по желанию.

Где обязательна геометрия, вертикальные стены и угол 90 градусов

Геометрия помещения в бюджетных ремонтах обязательная лишь в 2-х местах, а остальное по желанию. Первое место — это кухня, а именно 2 стены, где будут висеть шкафы и ванная комната, желательно вся, если производится укладка плитки. Под ПВХ-панели можно попробовать и не выравнивать, но это опять же будет хуже качество. Можно вообще не выравнивать, но качество будет ещё хуже! В общем, я надеюсь мысль понятна: если хотите хорошее качество — нужно выровнять.