Лямбда стали – Удельная теплота плавления – формула, таблица единиц измерения для вещества

Удельная теплота плавления — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 июля 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 июля 2019; проверки требуют 2 правки.

Уде́льная теплота́ плавле́ния (также: энтальпия плавления; также существует равнозначное понятие уде́льная теплота́ кристаллиза́ции) — количество теплоты, которое необходимо сообщить одной единице массы кристаллического вещества в равновесном изобарно-изотермическом процессе, чтобы перевести его из твёрдого (кристаллического) состояния в жидкое (то же количество теплоты выделяется при кристаллизации вещества).

Единица измерения — Дж/кг. Теплота плавления — частный случай теплоты термодинамического фазового перехода.

Удельная теплота плавления обозначается буквой λ{\displaystyle \lambda } (греческая буква

лямбда). Формула расчёта удельной теплоты плавления:

λ=Qm,{\displaystyle \lambda ={\frac {Q}{m}},}

где Q{\displaystyle Q} — количество теплоты, полученное веществом при плавлении (или выделившееся при кристаллизации), m{\displaystyle m} — масса плавящегося (кристаллизующегося) вещества. Удельная теплота плавления всегда положительна; единственное известное исключение — гелий под высоким давлением^[1][2].

Значения удельной теплоты плавления некоторых веществ[править | править код]

• Енохович А. С. Краткий справочник по физике. — М.: «Высшая школа», 1976. — С. 114. — 288 с.

1. ↑ Atkins, Peter & Jones, Loretta (2008), Chemical Principles: The Quest for Insight (4th ed.), W. H. Freeman and Company, с. 236, ISBN 0-7167-7355-4 
2. ↑ Hoffer J. K., Gardner W. R., Waterfield C. G., Phillips N. E. Thermodynamic properties of ⁴He. II. The bcc phase and the P-T and VT phase diagrams below 2 K (англ.) // Journal of Low Temperature Physics (англ.)русск. : journal. — 1976. — April (vol. 23, no. 1). — P. 63—102. — DOI:10.1007/BF00117245. — Bibcode: 1976JLTP…23…63H.

Лямбда-зонд — Википедия

Лямбда-зонд (λ-зонд) — датчик остаточного кислорода (например, в выпускном коллекторе двигателя или дымоходе отопительного котла). Позволяет оценивать количество оставшегося не сгоревшего топлива либо кислорода в выхлопных газах. Данные показания позволяют приготовлять оптимальную воздушно-топливную смесь, а также снижать количество вредных для человека побочных продуктов процесса сгорания.

Лямбда-зонд порогового типа действует по принципу гальванического элемента/твердооксидного топливного элемента с твердым электролитом в виде керамики из диоксида циркония (ZrO

2). Керамика легирована оксидом иттрия, а поверх неё напылены токопроводящие пористые электроды из платины, одновременно являющейся катализатором окислительно-восстановительных реакций. Один из электродов омывается горячими выхлопными газами (внешняя сторона датчика), а второй — воздухом из атмосферы (внутренняя сторона датчика). Эффективное измерение состава отработавших газов лямбда-зонд обеспечивает после разогрева до определенной температуры выше 300°C. Только в таких условиях циркониевый электролит приобретает проводимость, а гальваническая ячейка начинает работать. Для работы датчика атмосферный кислород нужен в очень небольшом количестве, поэтому, в целом герметичный для воды, датчик делается таким образом, чтобы кислород немного попадал внутрь со стороны проводки.

Если при работе двигателя и датчика ионы свободного кислорода присутствуют лишь с внутренней стороны элемента, то есть имеется лишь атмосферный кислород, то разогретая ячейка самостоятельно начинает генерировать ЭДС, а значит, на блок управления с датчика начинает поступать электрический ток с определённым напряжением. Это означает для ЭБУ автомобиля, что смесь была «богатой». На практике этому соответствует примерно 0,8-0,9 вольт. Если свободный кислород появляется в составе выхлопа с внешней стороны датчика, то выработка ЭДС снижается, а если кислорода достаточно много, то полностью прекращается, то есть кислород из выхлопа блокирует работу ячейки. Это означает для ЭБУ, что смесь была «бедной». На практике этому соответствует примерно 0,1-0,2 вольт. Если ЭДС стремится к нулю, то это означает что смесь абсолютно бедная, например в двигатель не поступает топливо. Напряжение с датчика 0,45 вольт считается оптимальным, и свидетельствует, что сжигаемая смесь обладает стехиометрическим соотношением топлива и воздуха.

Конструктивно, датчики делятся по числу проводов и наличию подогревательного элемента. Датчики без нагревательного элемента используют 1 или 2 провода, с нагревательным элементом — 3 или 4 провода. Первое поколение датчиков разогревалось лишь от выхлопных газов, поэтому начинало давать сигнал сравнительно поздно после старта двигателя. Появившиеся позже датчики с нагревательным элементом стали выводить датчик в рабочее состояние очень быстро, что отвечало возросшим требованиям экологии, а также позволяло использовать датчик, когда температуры выхлопных газов оказывалось недостаточно.

В начале работы, после запуска мотора, лямбда-зонд не выдаёт показаний, и ЭБУ вынужден использовать только карты впрыска, прописанные в нём. Это режим работы без обратной связи, и коррекции топливной смеси по лямбда-зонду в этом режиме нет. Когда с датчика появляется сигнал, то ЭБУ автомобиля переходит в режим работы с обратной связью, при котором исходные топливные карты корректируются с учётом показаний с лямбда-зонда в режиме реального времени.

Сигнал используется системой управления для поддержания оптимального (стехиометрического, около 14,7:1) соотношения воздушно-топливной смеси.

• λ=1 — стехиометрическая (теоретически идеальная) смесь;
• λ>1 — бедная смесь;
• λ<1 — богатая смесь (избыток топлива, воздуха не хватает для полного сгорания).

Работа датчика не линейна во времени, показания отклоняются от оптимального очень быстро, поэтому ЭБУ вынужден постоянно корректировать смесь. При этом двигатель редко работает на идеальном стехиометрическом составе смеси, однако смесь постоянно стремится к достижению идеальной пропорции. Лямбда-зонд не сообщает о том, сколько именно кислорода в выхлопных газах, он сигнализирует о том, есть ли свободный кислород в выхлопе или нет. Факт наличия свободного кислорода и означает, что топлива в смеси должно быть больше, поскольку часть кислорода не вступила в реакцию. И наоборот, если кислорода нет или очень мало, то требуется уменьшить подачу топлива, тем более, что если топлива окажется слишком много, то это приведёт к появлению сажи и так называемого «грязного» выхлопа. В реальности, достичь и долго удерживать идеальную стехиометрическую смесь невозможно, так как существует множество факторов, постоянно влияющих на смесеобразование и её сгорание. Поэтому, целью является не само достижение стехиометрического соотношения, а стремление к этому, путём постоянной коррекции смеси и пребывания её поочередно то в «условно-бедном», то в «условно-богатом» состоянии, не отдаляясь от оптимального состава. Правильность работы датчика даёт возможность максимально сократить разницу между реальным соотношением воздуха/топлива и стехиометрическим.

График вольтажа с датчика обычно имеет вид синусоиды с довольно резким переходом от верхних значений к нижним, и наоборот. Принцип цикла таков: датчик сообщил, что смесь «бедная» — ЭБУ начинает постепенно добавлять топлива; далее датчик сообщает, что смесь стала «богатой» — ЭБУ начинает уменьшать подачу топлива, и так постоянно, пока активна обратная связь. Изменение подачи топлива (как реакция на показания лямбда-зонда) обычно выполняется с использованием двух переменных в ЭБУ — «долгая» коррекция и «краткая» коррекция, и они заложены в стандарт диагностики OBD-II. Краткая коррекция позволяет смеси следовать за датчиком сиюсекундно. Долгая коррекция вычисляется ЭБУ на основании анализа краткой коррекции, и нужна для того чтобы сдвигать всю коррекцию, фактически подстраиваясь под особенности и состояние конкретного образца мотора. Каждая коррекция может изменять впрыск в установленных производителем пределах, и если сумма долгой и краткой коррекций выйдет за общий предел, то обычно ЭБУ сигнализирует об ошибке смесеобразования с помощью индикатора «check engine». ЭБУ обычно использует режим работы с обратной связью по лямбда-зонду до определённого процента расчётной нагрузки на мотор. Далее ЭБУ временно прекращает режим коррекции, так как возникает вероятность неэффективной коррекции, и в этих условиях использование карт впрыска оказывается предпочтительным.

Поскольку некоторое количество кислорода должно присутствовать в выхлопе для нормального дожигания СО и СН^{[неизвестный термин]} в катализаторе, для более точного регулирования может использоваться и второй лямбда-зонд, расположенный за катализатором или внутри него.

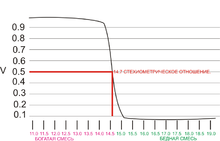
Разновидность кислородного датчика.

Основная разница зонда с широким диапазоном измерения по отношению к обычным узкополосным λ-зондам — это комбинация сенсорных ячеек и так называемых накачивающих ячеек. Состав его газового содержимого постоянно соответствует λ=1, что для сенсорной ячейки значит напряжение в 450 милливольт. Содержание газа в зазоре и вместе с ним напряжение сенсора поддерживаются посредством различных напряжений, прикладываемых к накачивающей ячейке. При бедной смеси и напряжении сенсора ниже 450 милливольт ячейка выкачивает кислород из диффузионной полости. Если смесь богатая и напряжение лежит выше 450 милливольт, ток меняет своё направление, и накачивающие ячейки транспортируют кислород в диффузионные расщелины. При этом интегрированный нагревающий элемент устанавливает температуру области от 700 до 800 градусов. Датчик типа LSU при погружении в несгоревшую смесь, содержащую одновременно и топливо и кислород, будет указывать «избыток воздуха», в отличие от порогового, сигнал которого надо интерпретировать «избыток топлива».

Выходной сигнал широкодиапазонного датчика зависит от его контроллера управления, может быть токовым или потенциальным. Например, выходной ток контроллера широкополосного датчика I_pn и соответствующие значения λ^[1]:

Ipn, мА	−5.000	−4.000	−3.000	−2.000	−1.000	−0.500	0.000	0.500	1.000	1.500	2.000	2.500	3.000	4.000
λ	0.673	0.704	0.753	0.818	0.900	0.948	1.000	1.118	1.266	1.456	1.709	2.063	2.592	5.211

Основным преимуществом широкополосного зонда по отношению к узкополосному является устранение циклического перехода дискретных показаний «бедная смесь — богатая смесь». Блок управления получает информацию о степени несоответствия смеси оптимальному значению, и это ему позволяет точнее и быстрее корректировать смесь для достижения её полного сгорания без свободного кислорода.

Лямбда Возничего — Википедия

Звезда
Лямбда Возничего, λ Возничего
Место звезды в созвездии указано стрелкой и обведено кружком
Тип	Одиночная звезда
Прямое восхождение	05ч 19м 8,47с[1]
Склонение	+40° 05′ 56,58″[1]
Расстояние	41,2±0,1 св. года (12,63±0,04 пк)[a]
Видимая звёздная величина (V)	4.71[2]
Созвездие	Возничий
Лучевая скорость (Rv)	66,5[3] км/c
Собственное движение
• прямое восхождение	+518,99 ± 0,26[1] mas в год
• склонение	-665,06 ± 0,13[1] mas в год
Параллакс (π)	79.17 ± 0.28[1] mas
Абсолютная звёздная величина (V)	4.20[4]
Спектральный класс	G1V[5]
Показатель цвета
• B−V	+0.62[2]
• U−B	+0.13[2]
Масса	1,081++0,054 −-0,029[6] M⊙
Радиус	1,331 ± 0,021[5] R⊙
Возраст	4,[7] 5,0–7,9 млрд,[8] лет
Температура	5 890 ± 4,3[9] K
Светимость	1,732 ± 0,022[5] L⊙
Металличность	+0.12[7]
Вращение	2 км/с[10]
Ba Лямбда Возничего, λ Возничего, Lambda Aurigae, λ Aurigae, λ Aur Fl 15 Возничего, 15 Aurigae BD +39 1248, CCDM J05192+4007A, FK5 1145, HD 34411, HIC 24813, HIP 24813, HR 1729, IRAS 05156+4003, PPM 47977, SAO 40233, 2MASS J05190848+4005565, GC 6494, GCRV 3155, GJ 807, IDS 05121+4001, LTT 403, N30 1135, PLX 1199, TD1 4327, TYC 2900-2157-1, UBV 5041, WDS J05191+4006A[11]
SIMBAD	данные
ARICNS	данные
Информация в Викиданных

Лямбда Возничего (λ Возничего, Lambda Aurigae, сокращ. lam Aur, λ Aur) — звезда в северном созвездии Возничий. Звезда имеет видимую звёздную величину 4.71^m[2], и, согласно шкале Бортля, видна невооружённым глазом на пригородном небе.

Из измерений параллакса, полученных во время миссии Hipparcos, известно, что звезда удалена примерно на 41,2 св. лет (12,63 пк) от Солнца^[1]. Звезда наблюдается севернее 50° ю. ш., то есть практически на всей территории обитаемой Земли, за исключением приполярных областей Антарктиды. Лучшее время наблюдения — декабрь^[12].

λ Aurigae — (латинизированный вариант лат. Lambda Aurigae) является обозначением Байера. У звезды также имеется обозначение данное Флемстидом — 15 Aurigae.

Звезда, возможно, была названа «Аль Хурр», что означает «олень» по-арабски^[13]. λ Возничего, наряду с µ Возничего и ρ Возничего входила в астеризм «Палатка» англ. Al Ḣibāʽ (араб. ألحباع‎), как это было приведено у Казвини^[13]. Согласно каталогу звёзд в Техническом меморандуме 33-507 — сокращённый каталог звёзд, содержащий 537 названных звёзд — Al Ḣibāʽ был названием для трёх звёзд: λ Возничего как Al Ḣibāʽ I, µ Возничего как Al Ḣibāʽ II и σ Возничего как Al Ḣibāʽ III^[14].

В китайской астрономии (англ.)русск., звезда относится к созвездию «Сеть» (англ.)русск. и астеризму 咸池 (Xián Chí), что означает «Область Гармонии» (англ. Pool of Harmony), состоящему из Лямбда Возничего, Ро Возничего и HD 36041^[15]. Следовательно, сама Лямбда Возничего известна как 咸池三 (Xián Chí sān, англ. the Third Star of Pool of Harmony — «Третья звезда Области Гармонии»)^[16].

Лямбда Возничего — жёлтый карлик спектрального типа G1V^[5], что указывает на то, что звезда использует водород в своём ядре в качестве ядерного «топлива». По составу звезда очень похожа на Солнце, а по массе и радиусу немного больше^[6]. Звезда имеет поверхностную гравитацию 4,02 СГС^[17] или 104,7 м/с², то есть почти в три раза меньше, чем на Солнце (274,0 м/с². Она на 73 % ярче Солнца^[5] и излучает энергию со своей внешней атмосферы при эффективной температуре около 5890 К^[9], что придаёт ей желтоватый оттенок звезды G-типа^[18].

Для того чтобы планета, аналогичная нашей Земле, получала примерно столько же энергии, сколько она получает от Солнца, её надо было бы поместить на расстоянии 1,35 а.е. (то есть несколько ближе Марса, чей радиус орбиты равен 1,56 а.е.). Причём с такого расстояния Лямбда Возничего выглядела бы на 25 % меньше нашего Солнца, каким мы его видим с Земли — 0,75° (угловой диаметр нашего Солнца — 0,5°)^[19].

Лямбда Возничего имеет низкий уровень поверхностной активности и находится в состоянии аналогичным минимуму Маундера на Солнце^[20], возможно, в результате большого возраста (звезды, становясь старше, вращаются медленнее, в результате магнитного торможения)^[21].

Вращаясь с экваториальной скоростью 2 км/с (то есть со скоростью практически равной солнечной), этой звезде требуется порядка 35 дней, чтобы совершить полный оборот. В результате сочетания массы (на 7 % больше чем у Солнца) и светимости (поскольку звезды главной последовательности по мере увеличения возраста становится ярче), возраст Лямбда Возничего можно оценить в 6 2 млрд. лет (то есть на 1 7 млрд. лет старше Солнца). Учитывая теоретическое время жизни звезды в 8 млрд. лет, звезде, хотя в настоящее время она и остаётся настоящим карликом, осталось не так много времени, чтобы закончить ядерный синтез и стать настоящим субгигантом, как и всем звёздам её класса^[21].

К сожалению, у звезды не обнаружено каких-либо планет, по крайней мере пока, хотя сама Лямбда Возничего, в некоторой степени, богата металлами (звезды, имеющие планеты, имеют тенденцию иметь больше металлов), а содержание железа (относительно водорода) на 15 % больше, чем у Солнца. Большинство других химических элементов также довольно велико, хотя азот и углерод несколько подавлены^[21].

Лямбда Возничего была исследована на наличие избыточного инфракрасного излучения, которое может указывать на наличие околозвёздного диска из пыли, но никакого существенного избытка не наблюдалось^[7]. Звезда является возможным членом движущейся группы звёзд Эпсилон Индейца, члены которой имеют общее движение в пространстве. Компоненты пространственной скорости для этой звезды [U,V,W] = [+76,-39,-6] км/с, то есть во много раз больше, чем у окружающих Солнце звёзд^[22].

Двойственность звезды открыл В. Я. Струве в 1836 году (современный компонент AD). Согласно Вашингтонскому каталогу визуально-двойных звёзд, параметры этих компонентов приведены в таблице^[23]:

Однако, у звезды, похоже, нет спутников. Хотя в таблице и перечислено четыре спутника (14-ой величины Лямбда Возничего B на расстоянии 29.1″, 13-ой величины Лямбда Возничего C на расстоянии 41.7″ и 9-ой величины Лямбда Возничего D и E на расстояниях 146.6″ и 168.8″), их движения показывают, что эти звёзды движутся очень быстро, и, скорее всего, они не имеют гравитационной связи с Лямбда Возничего, то есть все они находится на линии прямой видимости. Само движение Лямбда Возничего, тем не менее, показывает, что звезда это посетитель из другой части Галактики, так как звезда движется с огромной скоростью 76 км/с относительно Солнца, что почти в пять раз больше, чем у местных звёзд Галактического диска^[21].

Следующие звёздные системы находятся на расстоянии в пределах 20 световых лет^[24] от системы Лямбда Возничего (включены только: самая близкая звезда, самые яркие (<6,5^m) и примечательные звёзды). Их спектральные классы приведены на фоне цвета этих классов (эти цвета взяты из названий спектральных типов и не соответствуют наблюдаемым цветам звёзд):

Рядом со звездой, на расстоянии 20 световых лет, есть ещё порядка 25 красных, оранжевых и жёлтых карликов спектрального класса M, K, G и 2 белых карлика, которые в список не попали.

Комментарии

1. ↑ Расстояние рассчитано по приведённому значению параллакса

Источники

1. ↑ ^{1 2 3 4 5 6}  (англ.) van Leeuwen, Floor (November 2007), «Validation of the new Hipparcos reduction», Astronomy and Astrophysics Т. 474 (2): 653–664, DOI 10.1051/0004-6361:20078357  Note: see VizieR catalogue I/311.
2. ↑ ^{1 2 3 4}  (англ.) Johnson, H. L.; Iriarte, B.; Mitchell, R. I. & Wisniewskj, W. Z. (1966), «UBVRIJKL photometry of the bright stars», Communications of the Lunar and Planetary Laboratory Т. 4 (99) 
3. ↑  (англ.) Nordström, B.; Mayor, M.; Andersen, J. & Holmberg, J. (May 2004), «The Geneva-Copenhagen survey of the Solar neighbourhood. Ages, metallicities, and kinematic properties of ˜14 000 F and G dwarfs», Astronomy and Astrophysics Т. 418: 989–1019, DOI 10.1051/0004-6361:20035959 
4. ↑  (англ.) Holmberg, J.; Nordström, B. & Andersen, J. (July 2009), «The Geneva-Copenhagen survey of the solar neighbourhood. III. Improved distances, ages, and kinematics», Astronomy and Astrophysics Т. 501 (3): 941–947, DOI 10.1051/0004-6361/200811191 
5. ↑ ^{1 2 3 4 5}  (англ.) Boyajian, Tabetha S.; McAlister, Harold A.; van Belle, Gerard & Gies, Douglas R. (February 2012), «Stellar Diameters and Temperatures. I. Main-sequence A, F, and G Stars», The Astrophysical Journal Т. 746 (1): 101, DOI 10.1088/0004-637X/746/1/101 . See Table 10.
6. ↑ ^{1 2}  (англ.) Takeda, Genya; Ford, Eric B.; Sills, Alison & Rasio, Frederic A. (February 2007), «Structure and Evolution of Nearby Stars with Planets. II. Physical Properties of ~1000 Cool Stars from the SPOCS Catalog», The Astrophysical Journal Supplement Series Т. 168 (2): 297–318, DOI 10.1086/509763 
7. ↑ ^{1 2 3}  (англ.) Greaves, J. S.; Wyatt, M. C. & Bryden, G. (August 2009), «Debris discs around nearby solar analogues», Monthly Notices of the Royal Astronomical Society Т. 397 (2): 757–762, DOI 10.1111/j.1365-2966.2009.15048.x 
8. ↑  (англ.) Mamajek, Eric E. & Hillenbrand, Lynne A. (November 2008), «Improved Age Estimation for Solar-Type Dwarfs Using Activity-Rotation Diagnostics», The Astrophysical Journal Т. 687 (2): 1264–1293, DOI 10.1086/591785 
9. ↑ ^{1 2}  (англ.) Kovtyukh, V. V.; Soubiran, C.; Belik, S. I. & Gorlova, N. I. (2003), «High precision effective temperatures for 181 F-K dwarfs from line-depth ratios», Astronomy and Astrophysics Т. 411 (3): 559–564, DOI 10.1051/0004-6361:20031378 
10. ↑  (англ.) Takeda, Yoichi; Sato, Bun’ei; Kambe, Eiji & Masuda, Seiji (February 2005), «High-Dispersion Spectra Collection of Nearby F—K Stars at Okayama Astrophysical Observatory: A Basis for Spectroscopic Abundance Standards», Publications of the Astronomical Society of Japan Т. 57 (1): 13–25, DOI 10.1093/pasj/57.1.13 
11. ↑  (англ.) * lam Aur — High proper-motion Star, Centre de Données astronomiques de Strasbourg, <http://simbad.u-strasbg.fr/simbad/sim-id?Ident=lam+Aur>. Проверено 27 января 2019. 
12. ↑ HR 1729 (рус.). Каталог ярких звезд.
13. ↑ ^{1 2} Allen, R. H. Star Names: Their Lore and Meaning (англ.). — Reprint. — New York, NY: Dover Publications Inc, 1963. — P. 91. — ISBN 0-486-21079-0.
14. ↑  (англ.) Rhoads, Jack W. (November 15, 1971), Technical Memorandum 33-507-A Reduced Star Catalog Containing 537 Named Stars, California Institute of Technology: Jet Propulsion Laboratory, <https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19720005197_1972005197.pdf>. Проверено 19 августа 2012. 
15. ↑  (кит.) 中國星座神話, written by 陳久金. Published by 台灣書房出版有限公司, 2005, ISBN 978-986-7332-25-7.
16. ↑  (кит.) AEEA (Activities of Exhibition and Education in Astronomy) 天文教育資訊網 2006 年 7 月 13 日
17. ↑  (англ.) Chen, Y. Q.; Nissen, P. E.; Zhao, G. & Zhang, H. W. (February 2000), «Chemical composition of 90 F and G disk dwarfs», Astronomy and Astrophysics Supplement Т. 141: 491–506, DOI 10.1051/aas:2000124 
18. ↑  (англ.) The Colour of Stars, Commonwealth Scientific and Industrial Research Organisation, December 21, 2004, <http://outreach.atnf.csiro.au/education/senior/astrophysics/photometry_colour.html>. Проверено 16 января 2012.  Архивировано 10 марта 2012 года.
19. ↑ Lambda Aurigae (англ.). Internet Stellar Database.
20. ↑  (англ.) Lubin, Dan; Tytler, David & Kirkman, David (March 2012), «Frequency of Maunder Minimum Events in Solar-type Stars Inferred from Activity and Metallicity Observations», The Astrophysical Journal Letters Т. 747 (2): L32, DOI 10.1088/2041-8205/747/2/L32 
21. ↑ ^{1 2 3 4}  (англ.) Kaler, James B., LAMBDA AUR (Lambda Aurigae), University of Illinois, <http://stars.astro.illinois.edu/sow/lambdaaur.html> 
22. ↑  (англ.) Kovacs, N. & Foy, R. (August 1978), «A detailed analysis of three stars in the Eggen’s Epsilon INDI moving group», Astronomy and Astrophysics Т. 68 (1–2): 27–31 
23. ↑ l Aurigae (англ.). Alcyone Bright Star Catalogue.
24. ↑ Stars within 20 light-years of Lambda Aurigae: (англ.). Internet Stellar Database.

Что такое лямбда? 11-я буква греческого алфавита :: SYL.ru

В настоящее время древнегреческий язык утратил многие признаки категории живого языка. Однако до сих пор на страницах школьных учебников, монастырских и церковных книг можно обнаружить древнегреческие слова и символы, используемые в качестве обозначения определенных величин.

За время своего существования древнегреческий язык сыграл большую роль в развитии мировой письменности и предопределил развитие некоторых мировых языков.

Интерес к языку подпитывается нередкими исследованиями алфавита, правил правописания и произношения. В данной статье узнаем, что представляет собой 11-я буква греческого алфавита – лямбда.

Наука и Греция

Алфавит, изобретенный греками, основан на финикийской и древнегреческой азбуке. Его основная особенность заключается в содержании двух типов букв – согласных и гласных. Прошло более двух десятков веков, но алфавит сохранился.

В научной среде греческий алфавит занимает прочное место. Во многих отраслях знаний его буквы можно обнаружить в качестве обозначения некоторых показателей. В математике синус угла обозначается α, используется знак суммы Σ. В астрономии в названии самых крупных звезд ярких созвездий упоминается α (альфа Большого Пса). В биологии при изучении групп особей активно используются понятия омега-самка и альфа-самец. В разделе ядерной физики можно встретиться с понятиями гамма-частицы и альфа-излучения. На страницах учебников химии и физики в качестве постоянных величин фигурируют ρ и λ, которыми обозначают плотность материала и длину волны соответственно. О последней букве расскажем подробнее, то есть ответим на вопросы о том, как пишется лямбда, откуда берет происхождение и где применяется.

Правописание

В первых версиях греческого алфавита внешний вид лямбды отличался от современного представления, хотя общее сходство наблюдалось. Большинство вариаций написания были представлены двумя прямыми линиями, одна из которых незначительно короче другой, а их концы сходятся. В восточном алфавите угол соединения находился в верхнем углу, в западном – в левом нижнем. Впоследствии римляне определились, что угол у них будет внизу слева, а греки решили, что он будет сверху. Последующий вариант содержал в себе вертикальный штрих с наклонной линией, уходящей вправо. В настоящее время букву лямбду прописную пишут согласно последнему описанному варианту, а заглавная выглядит в виде перевернутого знака V. На основе греческой лямбды образовалась латинская лямбда, заглавный символ которой представлен в виде перевернутого Y.

Значение

Лямбда образовалась от буквы финикийского алфавита – ламед. Данному символу в числовой алфавитной системе соответствовало число 30, которое в Греции приписывали справа сверху около вертикальной линии символа. На основании буквы лямбды образовались кириллическая Л и латинская L, а после и производные последних.

Использование прописной буквы

Области применения прописной версии буквы довольно обширны. Раньше символ можно было обнаружить на щитовых узорах спартанских войск. Сейчас он сохранился при обозначении вида частиц в физике, а в математике он представляет собой диагональную матрицу из собственных значений и выступает вводимыми операторами. Такое описание поясняет, что такое лямбда прописная и где она используется.

Строчная лямбда

Строчная буква λ закрепилась и занимает прочное место в физических формулах алгебры, физики, химии, информатики. Удельная теплота плавления, постоянная распада, длина волны, значение Ламе, линейная плотность электрического заряда – это те переменные, которые для простоты заменены этим символом. В биологии изучается вирус фаг лямбда. В информатике функциональные выражения производят в λ-исчислении. В самолетостроении при удлинении крыла вводится буква лямбда. В линейной алгебре найденные корни дифференциального уравнения также обозначаются через нее.

Каждый современный автомобилист знаком с лямбда-зондом, установленным в его транспортном средстве. Прибор измеряет количество образуемого углекислого газа в выхлопе. Оснащение автомобиля данным датчиком произошло по причине того, что власти многих стран заботятся об экологической составляющей и здоровье нации и таким образом регулируют количество выделяемого автомобилем СО₂. В случае критичности значения этого показателя, то есть его превышения относительно допустимой величины, в качестве жесткой меры выписывается штраф. Этот датчик также необходим для соблюдения оптимального и экономного расхода топлива.

Связь с культурной сферой

Что такое лямбда в культурной среде? В известном кинофильме «Звездные войны» путешествовал космический корабль класса лямбда. Буква также используется в компьютерных играх под эмблемой «Комплекс Лямбда». По мере развития сюжета игры она применяется в качестве знака противоборства между населением и альянсом. Символ существует и в эмблеме игр, строчная буква лямбда нередко фигурирует в слове Half-Life, в итоге получается Hλlf-Life.

В романтической песне под названием «Австралия» Михаила Щербакова герой мечтал завести кенгуру, муравьеда или жирафа по имени Лямбда.

В 1970 году, когда регулярно стали проходить гей-парады, значок лямбда был впервые использован в Нью-Йорке в качестве обозначения правозащитной организации «Альянс гей-активистов». Через четыре года в Шотландии Международным конгрессом прав геев «λ» признана интернациональным знаком движения за свободу и права людей с нетрадиционной ориентацией.

В настоящее время под знаком лямбды в культуре понимают объединение именно таких людей. Активисты при объяснении, почему именно этот символ выбран ключевым для описания их движения, ссылаются на физическое понятие длины волны. Они видят аналогию с волной, направленной в пространство и бесконечность, и считают, что лямбда является удачным обозначением для описания предстоящих изменений в социуме, в котором лиц нетрадиционной ориентации должны принять.

Сакральное значение

Что такое лямбда в эзотерическом плане? Лямбда заключает в себе принцип органического роста и переход системы на возвышенный уровень. Это подтверждается примерами двух видов прогрессий, ключевых числовых последовательностей древнегреческой математики, где используется знак. В теоретическом плане буква символизирует возрастание числовых рядов, которыми описывается любая система физических явлений. Каждый, рассматривая руны, обозначающие возвышение и означающие звук «Л» или древнееврейский знак ламед, обнаружит сходство с исследуемой буквой.

В данной статье было рассмотрено, что такое лямбда, и где ее можно встретить в окружающем мире.

что это, принцип работы, описание, драгоценные металлы в нем

С каждым годом количество автомобилей растет, что самым неблагоприятным образом сказывается на экологической ситуации. Страдают от загазованного воздуха не только жители крупных городов, но и вся планета в целом, поскольку озоновый защитный слой атмосферы становится все меньше. По этой причине в цивилизованном мире установлены жесткие правила, требующие установки на автомобилях катализаторов – устройств, поглощающих токсичные компонента выхлопных газов. Это несгоревшие углеводороды, окись углерода и окислы азота.

Катализатор – устройство полезное, но для его эффективной работы нужно создать соответствующие условия. Необходимо постоянно контролировать качество топливно-воздушной смеси.

Что это такое

Оптимальный состав топливно-воздушной смеси содержит 1 часть бензина на 14,7 частей атмосферного воздуха. Если принять такое соотношение за единицу, то его отклонение в большую/меньшую сторону свидетельствует об обогащенном или обедненном составе смеси. Чтобы катализатор работал максимально эффективно, отклонение от оптимальной единицы должно быть не более одного процента.

Технически проблема решается посредством установки встроенного в электронную систему подачи топлива лямбда-зонда, который поддерживает состав топливно-воздушной смеси в катализаторе в оптимальных пределах.

Принцип работы лямбда-зонда

Конструкция датчика состоит из следующих основных элементов:

• металлический корпус;
• керамический изолятор;
• электрический нагреватель;
• электропроводка и токопроводящие контакты.

В процессе работы двигателя внутреннего сгорания содержание кислорода в атмосферном воздухе и в выпускном коллекторе выхлопной системы разное. Один электрод лямбда-датчика «дышит» наружным воздухом, а второй выхлопными газами. Соответственно, ионы кислорода создают в твердом электролите разность потенциалов. Это напряжение передается на бортовую систему управления подачей топлива, в результате чего в режиме реального времени оптимизируется состав топливно-воздушной смеси.

Корректное измерение отклонения количества кислорода в катализаторе возможно только при температуре не ниже 300 градусов. Это обусловлено тем, что циркониевый электролит при меньшей температуре в качестве проводника не работает. Поэтому при холодном пуске лямбда-датчик не принимает участия, а за состав подаваемой в двигатель топливно-воздушной смеси на этом этапе отвечают иные электронные устройства. В современных датчиках кислорода имеется электрический подогрев управляемых бортовым электронным блоком.

Максимальная температура для работы лямбда-датчика также ограничена и не должна превышать 1000 градусов. Поэтому устройство, установленное для быстрого прогрева на выпускном коллекторе перед катализатором, чувствительно к перегреву вследствие длительной езды на максимальных оборотах двигателя.

Может ли работать автомобиль без лямбда-зонда

Ресурс кислородного датчика не превышает 80 000 км и зависит от исправности двигателя, условий эксплуатации автомобиля. Но больше всего на срок эксплуатации влияет качество топлива. Иногда достаточно израсходовать несколько баков некачественного бензина, и датчик перестает работать вообще.

Признаки неисправности катализатора:

• Холостые обороты самопроизвольно падают до 500-600. Причина – в систему поступает обедненная смесь, не обеспечивающая стабильность работы в режиме холостого хода.
• На ходу заметна существенная потеря мощности. Автомобиль с трудом набирает обороты, преодолевает подъемы, медленно разгоняется. Причина та же – некорректное содержание топливно-воздушной смеси.
• Расход увеличился на 20-30%. Из-за слишком обогащенной топливно-воздушной смеси наблюдается темный выхлоп с характерным запахом несгоревшего в катализаторе бензина. На свечах появляется налет черного цвета.
• При ускорении автомобиль дергается.
• На панели управления сигнализирует Check Engine. Теоретически ошибку можно сбросить, но от этого катализатор исправным не станет.

Причины неисправности:

• Топливо низкого качества. Чрезмерное количество примесей приводит к тому, что их несгоревшие остатки оседают на поверхности лямбда-датчика, нарушают токопроводимость его контактов.
• Превышен срок эксплуатации. В идеальных условиях устройство может корректно работать при пробеге 150 000 км и даже больше. В наших реалиях, как правило, не больше 80 000 км. Но это касается оригинального датчика. Ресурс некачественного лицензионного устройства предсказать практически невозможно.
• Неисправность электрической проводки, которая может повредиться по причине перегрева коллектора.

Что делать, если механизм вышел из строя

Прежде всего, нужно убедиться в неисправности лямбда-датчика. В этом плане проще и надежнее всего обратиться на станцию техобслуживания. Если есть желание и возможность, можно сделать визуальную проверку самостоятельно. Начать нужно с осмотра разъемов, проверки надежности их фиксации. Затем следует осмотреть кислородный датчик:

• сажа на корпусе – показатель сгорания обогащенной смеси или чрезмерного перегрева зонда;
• блестящие отложения создает топливо с избытком свинца;
• белый и серый налет возникает вследствие использования масляных и топливных присадок.

Что делать? Если на лямбда-датчике появился свинцовый налет, устройство подлежит замене, поскольку свинец повреждает не только зонд, но и катализатор. То же касается и налета от присадок. Если говорить о саже, то ее можно попробовать почистить своими руками с использованием ортофосфорной кислоты.

Какие драгоценные материалы содержатся в зонде

Керамический твердый электролит гальванического элемента изготовлен из диоксида циркония, легированного оксидом иттрия. Токопроводящие электроды имеют платиновое напыление.

Количество ценных драгметаллов ничтожно мало, и пытаться извлечь их в домашних условиях не имеет смысла. Негодный кислородный датчик может сослужить своему владельцу последнюю службу, если сдать катализатор в утиль. Компания «Лом-АКБ» принимает по выгодным ценам вышедшие из строя автомобильные детали от частных лиц и организаций.

Лямбда-исчисление — Википедия

Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем для формализации и анализа понятия вычислимости.

Чистое λ-исчисление, термы которого, называемые также объектами («обами»), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличие каких-либо констант не предполагается.

В основу λ-исчисления положены две фундаментальные операции:

• Абстракция или λ-абстракция (лат. abstractio — отвлечение, отделение) в свою очередь строит функции по заданным выражениям. Именно, если t≡t[x]{\displaystyle t\equiv t[x]} — выражение, свободно^[en] содержащее x{\displaystyle x}, тогда запись  λx.t[x]{\displaystyle \ \lambda x.t[x]} означает: λ{\displaystyle \lambda } функция от аргумента x{\displaystyle x}, которая имеет вид t[x]{\displaystyle t[x]}, обозначает функцию x↦t[x]{\displaystyle x\mapsto t[x]}. Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы x{\displaystyle x} свободно входило в t{\displaystyle t}, не очень существенно — достаточно предположить, что λx.t≡t{\displaystyle \lambda x.t\equiv t}, если это не так.

Основная форма эквивалентности, определяемая в лямбда-термах, это альфа-эквивалентность. Например, λx.x{\displaystyle \lambda x.x} и λy.y{\displaystyle \lambda y.y}: альфа-эквивалентные лямбда-термы и оба представляют одну и ту же функцию (функцию тождества). Термы x{\displaystyle x} и y{\displaystyle y} не альфа-эквивалентны, так как они не находятся в лямбда-абстракции.

Поскольку выражение λx.2⋅x+1{\displaystyle \lambda x.2\cdot x+1} обозначает функцию, ставящую в соответствие каждому x{\displaystyle x} значение 2⋅x+1{\displaystyle 2\cdot x+1}, то для вычисления выражения

(λx.2⋅x+1) 3{\displaystyle (\lambda x.2\cdot x+1)\ 3},

в которое входят и аппликация и абстракция, необходимо выполнить подстановку числа 3 в терм 2⋅x+1{\displaystyle 2\cdot x+1} вместо переменной x{\displaystyle x}. В результате получается 2⋅3+1=7{\displaystyle 2\cdot 3+1=7}. Это соображение в общем виде записывается как

(λx.t) a=t[x:=a],{\displaystyle (\lambda x.t)\ a=t[x:=a],}

и носит название β-редукция. Выражение вида (λx.t) a{\displaystyle (\lambda x.t)\ a}, то есть применение абстракции к некому терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ{\displaystyle \lambda }-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ{\displaystyle \lambda }-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.

η{\displaystyle \eta }-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи применёнными к любому аргументу, дают одинаковые результаты. η{\displaystyle \eta }-преобразование переводит друг в друга формулы λx.f x{\displaystyle \lambda x.f\ x} и f{\displaystyle f} (только если x{\displaystyle x} не имеет свободных вхождений в f{\displaystyle f}: иначе, свободная переменная x{\displaystyle x} после преобразования станет связанной внешней абстракцией или наоборот).

Функция двух переменных x{\displaystyle x} и y{\displaystyle y} f(x,y)=x+y{\displaystyle f(x,y)=x+y} может быть рассмотрена как функция одной переменной x{\displaystyle x}, возвращающая функцию одной переменной y{\displaystyle y}, то есть как выражение  λx.λy.x+y{\displaystyle \ \lambda x.\lambda y.x+y}. Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть выражены в λ{\displaystyle \lambda }-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг (также: каррирование), в честь американского математика Хаскелла Карри, хотя первым его предложил М. Э. Шейнфинкель (1924).

Семантика бестипового λ{\displaystyle \lambda }-исчисления[править | править код]

Тот факт, что термы λ{\displaystyle \lambda }-исчисления действуют как функции, применяемые к термам λ{\displaystyle \lambda }-исчисления (то есть, возможно, к самим себе), приводит к сложностям построения адекватной семантики λ{\displaystyle \lambda }-исчисления. Чтобы придать λ{\displaystyle \lambda }-исчислению какой-либо смысл, необходимо получить множество D{\displaystyle D}, в которое вкладывалось бы его пространство функций D→D{\displaystyle D\to D}. В общем случае такого D{\displaystyle D} не существует по соображениям ограничений на мощности этих двух множеств, D{\displaystyle D} и функций из D{\displaystyle D} в D{\displaystyle D}: второе имеет бо́льшую мощность, чем первое.

Эту трудность в начале 1970-х годов преодолел Дана Скотт, построив понятие области D{\displaystyle D} (изначально на полных решётках^[1], в дальнейшем обобщив до полного частично упорядоченного множества со специальной топологией) и урезав D→D{\displaystyle D\to D} до непрерывных в этой топологии функций^[2]. На основе этих построений была создана денотационная семантика^[en] языков программирования, в частности, благодаря тому, что с помощью них можно придать точный смысл таким двум важным конструкциям языков программирования, как рекурсия и типы данных.

Рекурсия — это определение функции через себя; на первый взгляд, лямбда-исчисление не позволяет этого, но это впечатление обманчиво. Например, рассмотрим рекурсивную функцию, вычисляющую факториал:

f(n) = 1, if n = 0; else n × f(n — 1).

В лямбда-исчислении, функция не может непосредственно ссылаться на себя. Тем не менее, функции может быть передан параметр, связанный с ней. Как правило, этот аргумент стоит на первом месте. Связав его с функцией, мы получаем новую, уже рекурсивную функцию. Для этого аргумент, ссылающийся на себя (здесь обозначен как r{\displaystyle r}), обязательно должен быть передан в тело функции.

g := λr. λn.(1, if n = 0; else n × (r r (n-1)))

f := g g

Это решает специфичную проблему вычисления факториала, но решение в общем виде также возможно. Получив лямбда-терм, представляющий тело рекурсивной функции или цикл, передав себя в качестве первого аргумента, комбинатор неподвижной точки возвратит необходимую рекурсивную функцию или цикл. Функции не нуждаются в явной передаче себя каждый раз.

Существует несколько определений комбинаторов неподвижной точки. Самый простой из них:

Y = λg.(λx.g (x x)) (λx.g (x x))В лямбда-исчислении, Y g{\displaystyle \operatorname {Y\ g} } — неподвижная точка g{\displaystyle \operatorname {g} }; продемонстрируем это:

Y g

(λh.(λx.h (x x)) (λx.h (x x))) g

(λx.g (x x)) (λx.g (x x))

g ((λx.g (x x)) (λx.g (x x)))

g (Y g).Теперь, чтобы определить факториал, как рекурсивную функцию, мы можем просто написать g (Y g)⁡n{\displaystyle \operatorname {g\ (Y\ g)} n}, где n{\displaystyle n} — число, для которого вычисляется факториал. Пусть n=4{\displaystyle n=4}, получаем:

g (Y g) 4
   (λfn.(1, if n = 0; and n·(f(n-1)), if n>0)) (Y g) 4
   (λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0)) 4
   1, if 4 = 0; and 4·(g(Y g) (4-1)), if 4>0
   4·(g(Y g) 3)
   4·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 3)
   4·(1, if 3 = 0; and 3·(g(Y g) (3-1)), if 3>0)
   4·(3·(g(Y g) 2))
   4·(3·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 2))
   4·(3·(1, if 2 = 0; and 2·(g(Y g) (2-1)), if 2>0))
   4·(3·(2·(g(Y g) 1)))
   4·(3·(2·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 1)))
   4·(3·(2·(1, if 1 = 0; and 1·((Y g) (1-1)), if 1>0)))
   4·(3·(2·(1·((Y g) 0))))
   4·(3·(2·(1·((λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 0))))
   4·(3·(2·(1·(1, if 0 = 0; and 0·((Y g) (0-1)), if 0>0))))
   4·(3·(2·(1·(1))))
   24

Каждое определение рекурсивной функции может быть представлено как неподвижная точка соответствующей функции, следовательно, используя Y{\displaystyle \operatorname {Y} }, каждое рекурсивное определение может быть выражено как лямбда-выражение. В частности, мы можем определить вычитание, умножение, сравнение натуральных чисел рекурсивно.

В языках программирования под «λ{\displaystyle \lambda }-исчислением» зачастую понимается механизм «анонимных функций» — callback-функций, которые можно определить прямо в том месте, где они используются, и которые имеют доступ к локальным переменным текущей функции (замыкание).

1. ↑ Scott D.S. The lattice of flow diagrams.— Lecture Notes in Mathematics, 188, Symposium on Semantics of Algorithmic Languages.— Berlin, Heidelberg, New York: Springer-Verlag, 1971, pp. 311—372.
2. ↑ Scott D.S. Lattice-theoretic models for various type-free calculi. — In: Proc. 4th Int. Congress for Logic, Methodology, and the Philosophy of Science, Bucharest, 1972.

• Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика: Пер. с англ. — М.: Мир, 1985. — 606 с.

Лямбда-точка — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 ноября 2015; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 ноября 2015; проверки требуют 5 правок.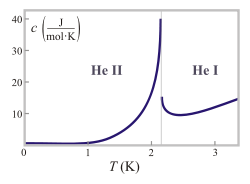 Лямбда-переход в жидком гелии: поведение удельной теплоёмкости при низких температурах

Лямбда-точка — температура (около 2,17 K), ниже которой жидкий гелий (гелий I), переходит в состояние сверхтекучести (гелий II).

Если быть более точным, существуют нижняя лямбда-точка (при 2,172 K и 0,0497 атм) и верхняя лямбда-точка (при 1,76 K и 29,8 атм).

Название происходит от специфического очертания графика удельной теплоёмкости как функции температуры (при постоянном давлении), напоминающее букву греческого алфавита λ. Удельная теплоёмкость имеет ярко выраженный пик по мере приближения температуры к лямбда-точке.

Ранние экспериментальные исследования теплоемкости^[1] привели к гипотезе, что она имеет логарифмическую особенность в лямбда-точке, и в частности стремится там в бесконечность. Более точные эксперименты^[2][3] опровергли эту гипотезу, которую к сожалению еще можно встретить в университетских учебниках.^[4] В настоящее время надежно установлено,^[5] что поведение теплоемкости вблизи лямбда-точки описывается формулой C≈A±t−α+B±{\displaystyle C\approx A_{\pm }t^{-\alpha }+B_{\pm }}, где t=|1−T/Tc|{\displaystyle t=|1-T/T_{c}|} есть приведенная температура, Tc{\displaystyle T_{c}} температура лямбда-точки, A±,B±{\displaystyle A_{\pm },B_{\pm }} константы принимающие различные значения выше и ниже точки перехода, а α≈−0.01{\displaystyle \alpha \approx -0.01} критический индекс. Так как этот индекс имеет отрицательное значение для перехода в сверхтекучее состояние, теплоемкость в лямбда-точке имеет конечные (хотя и большие) пределы при приближении с низких и высоких температур .^[6]

1. ↑ C. Buckingham and W.H. Fairbank. The Nature of the Lambda-Transition in Liquid Helium // Progress in Low Temperature Physics, vol. 3. — Amsterdam: North-Holland, 1961.
2. ↑ Guenther Ahlers. Heat Capacity at Constant Pressure near the Superfluid Transition in He 4 (англ.) // Physical Review Letters. — 1969-09-01. — Vol. 23, iss. 9. — P. 464—468. — ISSN 0031-9007. — DOI:10.1103/PhysRevLett.23.464.
3. ↑ K. H. Mueller, Guenter Ahlers, F. Pobell. Thermal expansion coefficient, scaling, and universality near the superfluid transition of He 4 under pressure (англ.) // Physical Review B. — 1976-09-01. — Vol. 14, iss. 5. — P. 2096—2118. — ISSN 0556-2805. — DOI:10.1103/PhysRevB.14.2096.
4. ↑ Квасников И.А. Термодинамика и статистическая физика. Том 1: Теория равновесных систем: Термодинамика. Учебное пособие. — Изд. 2-е, сущ. перераб. и доп.. — Москва: Едиториал УРСС, 2002. — С. 119. — 240 с. — ISBN 5-354-00077-7.
5. ↑ Lipa, J.A.; Swanson, D. R.; Nissen, J. A.; Chui, T. C. P.; Israelsson, U. E. Heat Capacity and Thermal Relaxation of Bulk Helium very near the Lambda Point (англ.) // Physical Review Letters : journal. — 1996. — Vol. 76, no. 6. — P. 944—947. — DOI:10.1103/PhysRevLett.76.944. — Bibcode: 1996PhRvL..76..944L. — PMID 10061591.
6. ↑ Теплоемкость обращается в бесконечность только для фазовых переходах второго рода с положительным индексом α{\displaystyle \alpha }. Например, это просиходит в критической точке жидкость-пар, которая имеет изинговские критические индексы.