Формула рабочий объем цилиндра – Объем цилиндра онлайн калькулятор: формула в м3 (кубах) и литрах — как посчитать через диаметр и высоту — Stoppanic

Содержание

Рассчитать объем цилиндра

Рассчитать объем цилиндра.

Рассчитать объем цилиндра вы можете по высоте и радиусу основания, высоте и площади основания, высоте и диаметру основания.

Калькулятор расчета объема цилиндра

Формулы расчета объема цилиндра

Цилиндр, виды цилиндров

Калькулятор расчета объема цилиндра:

Выберите, по каким параметрам вы хотите рассчитать объем цилиндра. Результат расчета получается в литрах, кубическим сантиметрах и кубических метрах.

Формулы расчета объема цилиндра:

Формула расчета объема цилиндра по высоте и радиусу основания:

V = π · r² · h,

где

V – объем цилиндра,

π – число пи, π ≈ 3,1415926535,

r – радиус основания,

h – высота цилиндра.

Формула расчета объема цилиндра по высоте и площади основания:

V = S · h,

где

V – объем цилиндра,

S – площадь основания цилиндра,

h – высота цилиндра.

Формула расчета объема цилиндра по высоте и диаметру основания:

V = π · d²/4h,

где

V – объем цилиндра,

π – число пи, π ≈ 3,1415926535,

d – диаметр цилиндра,

h – высота цилиндра.

Цилиндр:

Цилиндр (др.-греч. κύλινδρος – «валик, каток») – это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

В свою очередь цилиндрическая поверхность – это поверхность, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.

Основания цилиндра – это плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями.

Боковая поверхность цилиндра – это цилиндрическая поверхность между плоскостями оснований.

Виды цилиндров:

Прямой цилиндр – это цилиндр, у которого образующие перпендикулярны основанию.

Наклонный цилиндр – это цилиндр, у которого образующие не перпендикулярны основанию.

Круговой цилиндр – это цилиндр, основанием которого является окружность (круг).

Прямой круговой цилиндр – это цилиндр, который одновременно является и прямым, и круговым. Прямой круговой цилиндр – это тело вращения, которое получается при вращении прямоугольника на 360° вокруг его стороны, являющейся одновременно осью симметрии цилиндра.

У прямого кругового цилиндра образующая (l) равна его высоте (h).

Радиус цилиндра (r) – это радиус основания цилиндра.

Диаметр цилиндра (d) – это диаметр основания цилиндра.

Высота цилиндра (h) – это расстояние между основаниями цилиндра.

Ось симметрии прямого кругового цилиндра – это прямая, соединяющая центры окружности оснований цилиндра.

Осевое сечение прямого кругового цилиндра – это сечение прямого кругового цилиндра плоскостью, которая проходит через его ось. Данное сечение является прямоугольником.

Примечание: © Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности 52

Объём цилиндра. Калькулятор объёма цилиндра онлайн

Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.

Высота цилиндра — это отрезок, соединяющий две любые точки оснований но обязательно расположенный перпендикулярно к ним обоим.

Объем прямого цилиндра

Цилиндр — это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».

Объем цилиндра через радиус основания и высоту цилиндра

Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)

\[ \LARGE V = \pi \cdot R^{2} \cdot H \]

где:
V — объем цилиндра
π — число пи (3.1415)
R — радиус основания
H — высота цилиндра

Объем цилиндра через площадь основания и высоту цилиндра

Объем цилиндра равен произведению площади основания цилиндра на его высоту.

\[ \LARGE V = S \cdot H \]

где:
V — объем цилиндра
H — высота цилиндра
S — площадь цилиндра

Объем цилиндра через диаметр основания и высоту цилиндра

Объем цилиндра равен произведению диаметра основания и числа пи (3.1415) делённое на четыре высоты цилиндра

\[ \LARGE V = \frac {\pi \cdot D^{2} }{4 \cdot H} \]

где:
V — объем цилиндра
π — число пи (3.1415)
D — диаметр основания
H — высота цилиндра

Калькулятор объёма цилиндра

Входные данные

Радиус цилиндра r:

Высота цилиндра h:

Количество знаков после запятой в результате вычислений

1234567

Результат

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

РАБОЧИЙ ОБЪЁМ ЦИЛИНДРА — это… Что такое РАБОЧИЙ ОБЪЁМ ЦИЛИНДРА?

РАБОЧИЙ ОБЪЁМ ЦИЛИНДРА: РАБОЧИЙ ОБЪЁМ ЦИЛИНДРА — объём, освобождаемый поршнем при его движении от верхней мёртвой точки до нижней, равный произведению площади поршня на его рабочий ход (см.). Выражается в кубических метрах и литрах, а для мотоциклетных и лодочных подвесных двигателей — в кубических сантиметрах. Суммарный Р. о. всех цилиндров двигателя иногда называют литражом двигателя.

РАБОЧЕЕ ТЕЛО
РАБОЧИЙ ОРГАН МАШИНЫ

Смотреть что такое «РАБОЧИЙ ОБЪЁМ ЦИЛИНДРА» в других словарях:

рабочий объём цилиндра — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN displacement … Справочник технического переводчика
Рабочий объём — Для улучшения этой статьи желательно?: Викифицировать статью … Википедия
Рабочий объем — Рабочий объём (рабочий объём двигателя, литраж) один из важнейших конструктивных параметров (характеристик) двигателя внутреннего сгорания (ДВС), выражаемый в литрах (л) или кубических сантиметрах (см³). Литраж двигателя в значительной степени… … Википедия
Объём двигателя — 4 тактный цикл двигателя внутреннего сгорания Такты: 1.Всасывание горючей смеси. 2.Сжатие. 3.Рабочий ход. 4.Выхлоп. Двухтактный цикл. Такты: 1. При движении поршня вверх сжатие топливной смеси в текущем цикле и всасывание смеси для следующего… … Википедия
Гильза цилиндра — сменная цилиндрическая вставка, устанавливаемая в блок картере поршневых тепловых двигателей (См. Тепловой двигатель) с водяным охлаждением. Г. ц. изготовляют из чугуна и применяют в блоках из алюминиевых сплавов для уменьшения износа… … Большая советская энциклопедия
Бензиновый двигатель внутреннего сгорания — Бензиновый двигатель W16 Bugatti Veyron Бензиновые двигатели это класс двигателей внутреннего сгорания, в цилиндрах которых предварительно сжатая топливовоздушная смесь поджигается электрической и … Википедия
Четырехтактный двигатель — Бензиновые двигатели это класс двигателей внутреннего сгорания, в цилиндрах которых предварительно сжатая топливовоздушная смесь поджигается электрической искрой. Управление мощностью в данном типе двигателей производится, как правило,… … Википедия
Четырёхтактный мотор — Бензиновые двигатели это класс двигателей внутреннего сгорания, в цилиндрах которых предварительно сжатая топливовоздушная смесь поджигается электрической искрой. Управление мощностью в данном типе двигателей производится, как правило,… … Википедия
Поршневой двигатель внутреннего сгорания — 4 тактный цикл двигателя внутреннего сгорания Такты: 1. Всасывание горючей смеси. 2. Сжатие. 3. Рабочий ход. 4. Выхлоп. Двухтактный цикл. Такты: 1. При движении поршня вверх сжатие топливной смеси в … Википедия
Иж Планета — Общая информация Производитель Ижевский машиностроительный завод Годы выпуска 1962 1967 … Википедия

Объем цилиндра

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Объем правильного цилиндра через радиус и высоту цилиндра

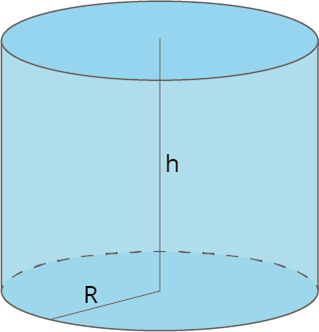
r — радиус основания цилиндра
h — высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Упрощение формулы:
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

S — площадь основания цилиндра
h — высота цилиндра

… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

d — диаметр основания цилиндра
h
— высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Теория

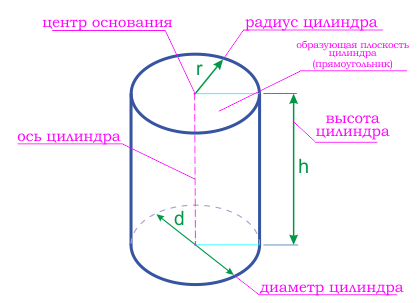
Цилиндр может быть правильным или наклонным.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Поверхности цилиндра

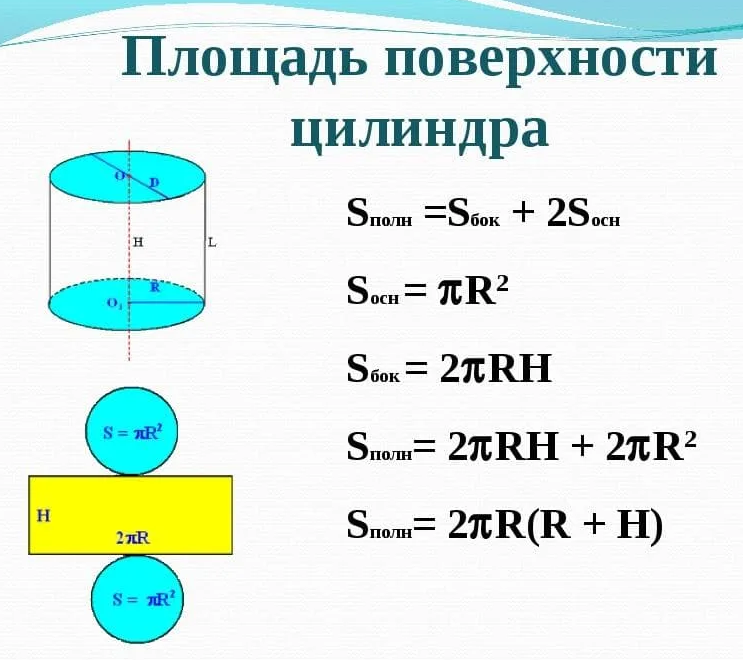
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Сечения цилиндра

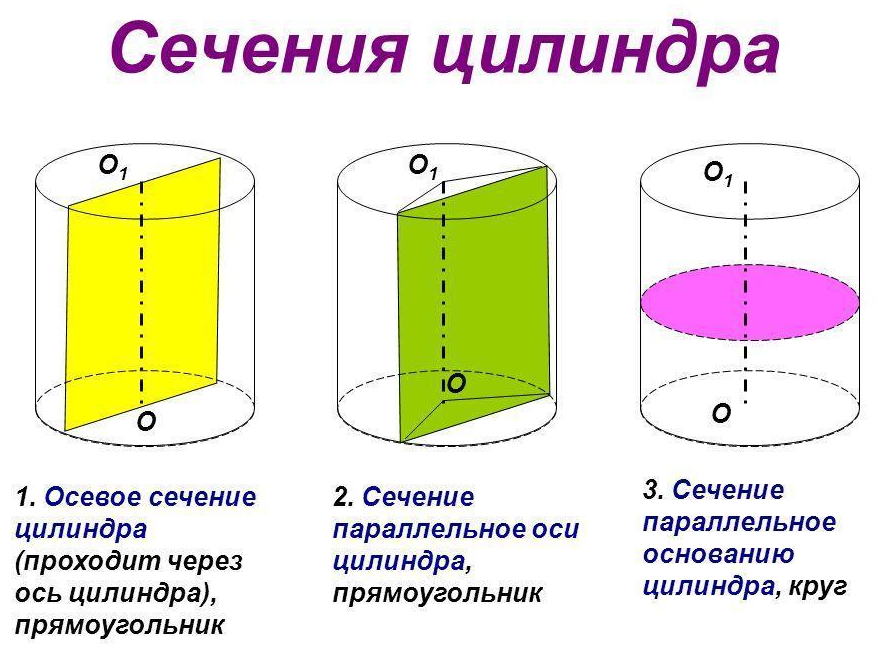
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся
прямоугольная фигура.
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг.
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс
.
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса.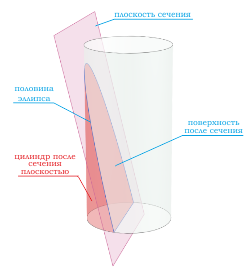

Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм³, см³, мл³.
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Объем полого цилиндра
Объем части цилиндра
Объем части полого цилиндра
Вы можете скачать формулы объема и площади поверхностей правильного цилиндра в виде картинки
Как посчитать объем цилиндра — онлайн калькулятор
Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор

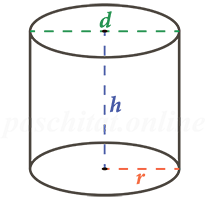
Найти чему равен объем цилиндра (V) можно зная (либо-либо):
радиус r и высоту h цилиндра

диаметр d и высоту h цилиндра

площадь основания S_o и высоту h цилиндра

площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.
Зная радиус r и высоту h
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
V = π⋅r²⋅h
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 2² ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см³
Зная диаметр d и высоту h
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
V = π⋅(^d/₂)²⋅h
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ (¹/₂)² ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см³
Зная площадь основания S_o и высоту h
Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?
Формула
V = S_o⋅h
Пример
Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см², то:
V = 10 ⋅ 5 = 50 см³
Зная площадь боковой поверхности S_b и высоту h
Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?
Формула
V = ^S_b²/_4πh
Пример
Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см², то:
V =^30²/_{4 ⋅ 3.14⋅ 5} = ⁹⁰⁰/_62.8 = 14.33 см³
Формула рабочего объема двигателя, цилиндра
Формула рабочего объема двигателя — это, по сути, формула рабочего объема цилиндра, умноженная на количество цилиндров двигателя. Но, поскольку она публиковалась в разных вариантах, то это может сбивать с толку. Независимо от используемого варианта формулы результат расчета будет одним и тем же.
Изменение рабочего объема двигателя после растачивания цилиндров или изменения хода поршней.
При растачивании цилиндров двигателя со стенок цилиндров снимается слой металла и штатные поршни заменяются ремонтными поршнями, имеющими больший диаметр. Растачивание цилиндров приводит к увеличению как рабочего объема, так и степени сжатия.
Серийный двигатель, уже использовавшийся в предыдущем примере расчета рабочего объема, с диаметром цилиндров 4,000 дюйма и ходом поршней 3,000 дюйма имеет рабочий объем 226 куб. дюймов. Если расточить цилиндры под диаметр, увеличенный на 0.060 дюйма, то диаметр цилиндров станет равным 4,060 дюйма.
Формула для расчета рабочего объема двигателя остается той же, за исключением того, что вместо 4,000 дюймов в нее подставляем 4,060 дюйма.
Рабочий объем двигателя (в кубических дюймах) = диаметр цилиндра х диаметр цилиндра х ход поршня х 0,7854 х число цилиндров
4.060 дюйма х 4,060 дюйма х 3,000 дюйма х 0,7854 х
х 6 = 233 кубических дюйма = 3818 см3.
Если диаметр цилиндров не изменяется, а ход поршней после замены коленчатого вала увеличится, то при этом возрастет как рабочий объем двигателя, так и степень сжатия цилиндров. Если ход поршней увеличивается на 1/8 дюйма (0,125 дюйма), а диаметр цилиндров остается таким же, как у серийного двигателя, расчет нового рабочего объема двигателя производится следующим образом:
Рабочий объем двигателя (в кубических дюймах) = диаметр цилиндра х диаметр цилиндра х ход поршня х 0,7854 х число цилиндров 4,000 дюйма х 4,000 дюйма х 3,125 дюйма х 0,7854 х х 6 = 236 кубических дюймов = 3867 см3.
Рабочий объем цилиндра формула двигателя
При одновременном увеличении диаметра цилиндров (расточены на 0,060 дюйма) и хода поршней (увеличен на 0,125 дюйма) рабочий объем двигателя в результате этих изменений станет равным.
4.060 дюйма х 4,060 дюйма х 3,125 дюйма х 0,7854 х
х 6 = 243 кубических дюйма = 3982 см3.
Формула объема цилиндра
Прежде чем говорить о формуле объема цилиндра разберемся с основополагающими моментами.
Цилиндр сам по себе является геометрической фигурой, которую ограничивают две находящиеся друг против друга области и пересекают цилиндрическую область. Данную цилиндрическую область можно получить путем направленных вперед движений образующих прямые линии так, чтобы образующая точка двигалась продольно направляющей кривой. Боковая область — та область фигуры которая ограничивается цилиндрической поверхностью. На основание приходиться другая часть, тем самым формы границы и направляющей совпадают.
Чаще всего это тело представляют в виде кругового прямого цилиндра, в котором окружность , прямая дающая направление и две основные области относительно образующей будут перпендикулярны. В данном теле будет ось симметрии.
Есть много типов цилиндров, которые различаются по форме основания, разрезу или наклону образующей. Бывают косые и наклонные, эллиптические, параболические и гиперболические.
Для того чтобы узнать объем цилиндра, необходимо знать высоту данного цилиндра или другими словами расстояние от одного основания до другого.

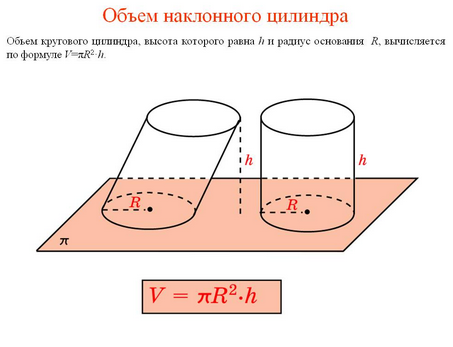
Объем цилиндра конечно же находиться при помощи формул, о которых и пойдет речь дальше. Для этого существуют две формулы: Формула объема цилиндра №1.
V = Sо*h
в которой V — это объем, Sо — площадь основания, h — это высота тела.

Формула объема цилиндра №2.
V = ? * R2 * h
в которой V — это объем, R — это радиус, h- это высота.
С помощью данной формулы, объем находится при помощи радиуса, числа ? и высоты. Данная формула применима только для кругового прямого цилиндра.
При использовании данных формул можно вычислить объем любой емкости, единственная поправка — это то что значения будут в метрах. А результат в кубических метрах.
Рассчитаем для наглядности
Дан цилиндр размер которого 0,5м. высота и диаметр 0,3м
Воспользуемся в расчетах формулой №2, в результате чего получаем:
V = 3,14 * 0,15 * 0,15 * 0,5 = 0,035325 кб/м
0,035325 кб/м = 35,325 литров.
Как видите в этом нет ничего сложного. Интересных вам вычислений!
Если вы ищите Полиуретан, пенополиуретан, оборудование для ППУ (http://puinfo.ru/), перейдите по ссылке на информационный сайт, в котором Вы найдете много нужной и интересной информации.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях: