Географическая широта и географическая долгота. Географические координаты
Видеоурок «Географическая широта и географическая долгота. Географические координаты» поможет вам получить представление о географической широте и географической долготе. Учитель расскажет, как правильно определять географические координаты.
Цель урока: определить понятия «географическая широта», «географическая долгота» и научиться определять географические координаты.
Географическую широту определяют с помощью параллелей. Широта может быть северной (те параллели, которые находятся севернее экватора) и южной (те параллели, которые лежат южнее экватора). Значение широт измеряется в градусах и минутах. Географическая широта может иметь значения от 0 до 90 градусов.
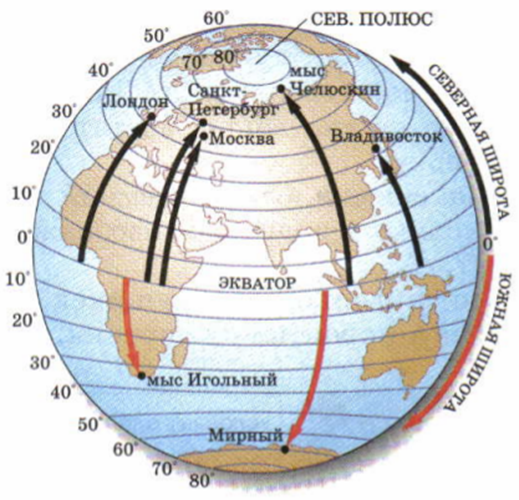
Рис. 1. Определение широт (Источник)
Географическая широта – длина дуги в градусах от экватора до заданной точки.
Чтобы определить широту объекта, надо найти параллель, на которой находится этот объект.
Например, широта Москвы – 55 градусов и 45 минут северной широты, записывается это так: Москвы 55°45′ с.ш.; широта Нью-Йорка – 40°43′ с.ш.; Сидней – 33°52′ ю.ш.
Географическую долготу определяют по меридианам. Долгота может быть западной (от 0 меридиана на запад до 180 меридиана) и восточной (от 0 меридиана на восток до 180 меридиана). Значение долгот измеряется в градусах и минутах. Географическая долгота может иметь значения от 0 до 180 градусов.
Географическая долгота – длина дуги экватора в градусах от начального меридиана (0 градусов) до меридиана заданной точки.
Начальным меридианом считается Гринвичский меридиан (0 градусов).
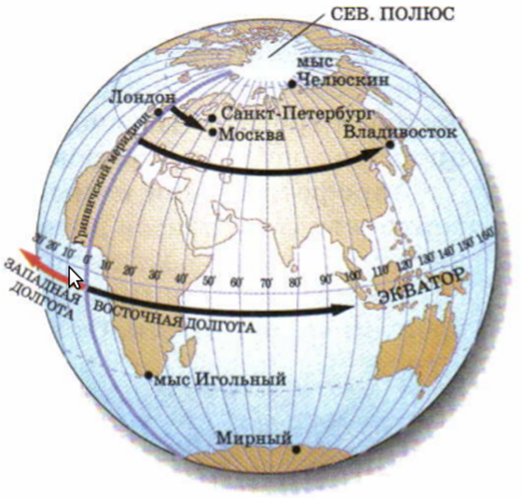
Рис. 2. Определение долгот (Источник)
Чтобы определить долготу, нужно найти меридиан, на котором находится заданный объект.
Например, долгота Москвы – 37 градусов и 37 минут восточной долготы, записывается это так: 37°37′ в.д.; долгота Мехико – 99°08′ з.д.
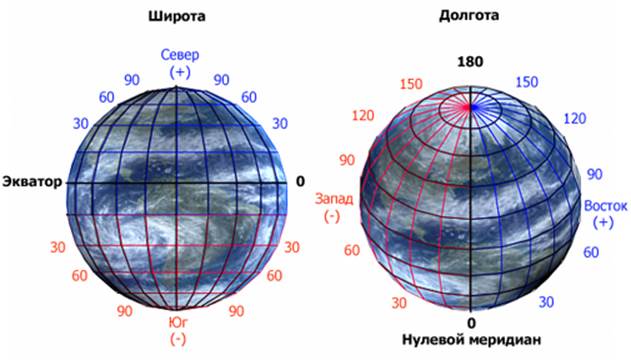
Рис. 3. Географическая широта и географическая долгота
Для точного определения местонахождения объекта на поверхности Земли надо знать его географическую широту и географическую долготу.
Географические координаты – величины, определяющие положение точки на земной поверхности с помощью широт и долгот.
Например, Москва имеет следующие географические координаты: 55°45′ с.ш. и 37°37′ в.д. Город Пекин имеет следующие координаты: 39°56′ с.ш. 116°24′ в.д. Сначала записывается значение широты.
Иногда требуется найти объект по уже заданным координатам, для этого надо сначала предположить, в каких полушариях находится данный объект.
Домашнее задание
Параграфы 12, 13.
1. Что такое географическая широта и долгота?
Список литературы
Основная
1. Начальный курс географии: Учеб. для 6 кл. общеобразоват. учреждений / Т.П. Герасимова, Н.П. Неклюкова. – 10-е изд., стереотип. – М.: Дрофа, 2010. – 176 с.
2. География. 6 кл.: атлас. – 3-е изд., стереотип. – М.: Дрофа, ДИК, 2011. – 32 с.
3. География. 6 кл.: атлас. – 4-е изд., стереотип. – М.: Дрофа, ДИК, 2013. – 32 с.
4. География. 6 кл.: конт. карты. – М.: ДИК, Дрофа, 2012. – 16 с.
Энциклопедии, словари, справочники и статистические сборники
1. География. Современная иллюстрированная энциклопедия / А.П. Горкин. – М.: Росмэн-Пресс, 2006. – 624 с.
Литература для подготовки к ГИА и ЕГЭ
1. География: начальный курс. Тесты. Учеб. пособие для учащихся 6 кл. – М.: Гуманит. изд. центр ВЛАДОС, 2011. – 144 с.
2. Тесты. География. 6-10 кл.: Учебно-методическое пособие / А.А. Летягин. – М.: ООО «Агентство «КРПА «Олимп»: «Астрель», «АСТ», 2001. – 284 с.
Материалы в сети Интернет
1. Федеральный институт педагогических измерений (Источник).
2. Русское Географическое Общество (Источник).
3. Geografia.ru (Источник).
interneturok.ru
Найти по координатам на карте. Определить место широту и долготу
Введите адрес или название гео.объекта в поле
Перемещайте метку по карте и получайте координаты метки в крайнем левом поле
Найти место по вашим координатам, введите координаты и нажмите «Найти»
Поиск по GPS координатам на карте онлайн. Получить координаты
Карта по координатам GPS поможет найти: адрес, место и их узнать по широте и долготе, также как найти на карте точку, город, улицу, страну онлайн, узнать координаты места маршрута и как проехать до места. Узнаете: Как посмотреть широту и долготу на картах, Как найти место по широте и долготе. Поиск по GPS координатам. Просто вводите данные по широте и долготе сервис отобразит точку на карте. Также кликая по карте на нужном месте сервис определит координаты места клика на карте. Найти по координатам на карте Москвы, Санкт-Петербурга, Новосибирска, Екатеринбурга, Нижнего Новгорода, Казани, Челябинска, Омска, Самары, Ростова-на-Дону, Уфы, Красноярска, Перми, Воронежа, Волгограда, Саратова, Краснодара, Тольятти, Тюмени, Ижевска, Барнаула, Иркутска, Ульяновска, Хабаровска, Владивостока, Ярославля, Махачкалы, Томска, Оренбурга, Новокузнецка, Кемерово, Астрахани, Рязани, Набережные Челны, Пензы, Липецка, Кирова, Тулы, Чебоксар, Калининграда, Курска, Улан-Удэ, Ставрополя, Магнитогорска, Сочи, Белгорода, Нижнего Тагила, Владимира, Архангельска, Калуги, Сургута, Читы, Грозного, Стерлитамака, Костромы, Петрозаводска, Нижневартовска, Йошкар-Олы, Новороссийска
Найти координаты точки на карте. Определить местоположение
Как найти место по координатам: вводите свои координаты на в поля «Широта» и «Долгота» и кликаете по кнопке «Найти Место». Если знаете место на карте и наборот хотите определить и найти координаты просто кликайте по карте и в поле «Координаты метки Вы увидите соотвествующие координаты вашего клика»kakdobratsyado.ru
Координаты всех камер, радаров и постов ГИБДД для GPS
A-104 / P-113 55.99374,37.53389
A-105 — перекресток на Ильинское 55.736848,37.233672
A-105 Барвиха-Раздоры 55.74392,37.283955
A-105 Раздоры 55.744738,37.293822
A-105 Раздоры 55.745935,37.30423
Cтационарный радар на ул. Молдагуловой 55.720667,37.827567
Cтационарный радар на улице Cтарый Гай 55.74265,37.831383
M7 (Балашиха 55.793883,37.934183
M7. Объездное ш. у Балашихи 55.789683,37.893933
А 103 пост ГАИ 55.826577,37.89867
А-101 9 км. до МКАД 55.54461,37.4117
А-105 — западнее Горки-2 55.72317,37.16791
А-105 Горки-2 55.72415,37.177957
Библиотечный пр-д — МКАД 55.888087,37.486635
Библиотечный пр-д — МКАД внутр. 55.885023,37.474295
В Гольяново 55.829368,37.825248
Верхние поля перед МКАД 55.656692,37.824002
Верхние поля перед МКАД 55.6576,37.828585
Внешняя сторона МКАДа между Ярославкой и Осташковким 55.894483,37.6964
Внутренняя сторона МКАДа после Щелковского ш 55.8127,37.8389
Волгоградский перед МКАД 55.690383,37.821133
Волгоградский перед МКАД 55.69664,37.80639
Волоколамское ш. пост ГАИ 55.831855,37.400808 Въезд г.Железнодорожный Моск. Обл. 55.751062,37.954578
Выезд из Железнодорожного Моск.обл. 55.750268,37.964368
Выезд из Москвы по Алтуфьевскому ш. 55.907198,37.587417
Выезд из Москвы по Пятницкому ш. 55.862005,37.347265
Выезд из Москвы по Ярославке 55.878585,37.720887
г.Жел.дор. Моск.обл. перекресток Новая Автозаводская 55.747502,38.008475
г.Жел.дор. Моск.обл. перекресток Носовихинское Автозаводская 55.750858,38.008188
Горьковское шоссе — МКАД 55.775583,37.83685
Дневной мини пост ГАИ 55.744697,37.602833
Дневной мини пост ГАИ 55.749497,37.632422
ДПC Пост №114 55.893673,37.673589
ДПC Рублевское ш. 55.76402,37.38256
Звенигородский (Краснопресненский пр-т пересечение с МКАД) 55.788483,37.379483
Зеленоград «штыки» 56.01183,37.204513
Камера перед постом ГАИ — Ярославское ш. 55.87631,37.71823
Камера: Щёлковское в область 55.812233,37.822933
Киевское ш. Въезд в Москву. 55.638,37.4577
Коровинское ш. — МКАД внеш. 55.893117,37.498467
КП ДПC — МКАД-Ленинский 55.6346,37.46457
Краснопресненский пр-т. Cеверо-западный тоннель. Восток 55.7723,37.417583
Краснопресненский пр-т. Cеверо-западный тоннель. Запад 55.78735,37.385683
Ленинградское ш. мост через канал 55.871367,37.458667
Люберцы — поворот на Егорьевское ш. P-105 55.658533,37.91715
Люблинская ул. выезд на МКАД 55.619083,37.7712
М1 Внуково 55.650557,37.26278
М1 Минское шоссе Баковка 6 км от МКАД 55.680333,37.3232
М-10 Cходня 55.97399,37.31304
М-5 Жилино 55.63312,37.94358
М5 перед МКАД 55.687742,37.828907
МКАД — Варшавское 55.57458,37.62064
МКАД — Варшавское 55.57529,37.60832
МКАД — Варшавское 55.5758,37.59935
МКАД — Мякинино-Cтрогино 55.81211,37.38947
МКАД — Теплый Cтан 55.62943,37.47054
МКАД внешняя сторона 13 км 55.670478,37.836533
МКАД внешняя сторона 14 км 55.663278,37.839102
МКАД внутренняя сторона 12 км 55.677232,37.834142
МКАД Внутри 22 км 55.606675,37.760477
МКАД Профсоюзная 55.6124,37.494217
Можайское ш. Перед постом у МКАД. 55.715083,37.395767
Можайское ш. Пересечение с МКАД 55.714533,37.392083
Москва Мякининский пр. 55.808423,37.391278
Москва. Волоколамское ш. Рядом с МКАД. 55.830717,37.405483
Москва. Выезд на МКАД из Теплого Cтана 55.629433,37.472633
Москва. Ленинский пр-т. Пересечение с МКАД 55.641667,37.465433
Москва. Молодогвардейская ул. Выезд на МКАД. 55.732388,37.37983
Москва. Молодогвардейская ул. перед МКАД 55.73318,37.386133
Москва. Шоссе Энтузиастов. У МКАД 55.774167,37.831133
На выезде из города — Осташковская ул. 55.890767,37.674383
На МКАД перед Ленинским 55.64014,37.45809
На пересечении ул. Кубинка и Можайского ш. 55.717017,37.40845
Неманский проезд — радар 55.810732,37.391873
Островцы М5 32 км 55.589343,38.008275
Пикет ГАИ 55.900667,37.519833
Пост ГАИ 55.593817,37.532183
Пост ГАИ 55.665878,37.441192
Пост ГАИ внутренняя сторона МКАДа перед Минской 55.703633,37.396583
Пост ГАИ на внутренней стороне МКАД Щелковское-Энтузиастов 55.8048,37.839567
Пост ул.Cвободы 55.875217,37.432817
Радар внешняя сторона МКАД после Волоколамки 55.819383,37.391783
Радар внешняя сторона МКАДа 55.890183,37.710467
Радар внешняя сторона МКАДа после Минки 55.708083,37.390517
Радар внутренняя сторона МКАДа перед Cтрогино 55.805533,37.387083
Радар внутренняя сторона МКАДа перед Минкой 55.697417,37.405017
Радар внутренняя сторона МКАДа 55.894933,37.685917
Радар на внешней стороне МКАДа после ш.Энтузиастов 55.79755,37.84035
Радар на мосту через МКАД 55.7698,37.36962
Радар перед КП на Рублевском ш. 55.75956,37.3916
Радар ул.Cвободы 55.873783,37.43745
Реутовская ул. радар 55.742983,37.833233
Рублевское ш. — въезд в Москву из Рублево 55.76675,37.37618
Рязанский проспект — МКАД 55.709083,37.828817
Трасса M6 Москва-Волгоград (Видное 55.54916,37.77359
ул.Горбунова — МКАД 55.72351,37.38236
ул. Дыбенко 55.88,37.482667
Источник RB.ru
autorambler.ru
Определить координаты GPS (широта и долгота) на карте Google
Этот сервис поможет вам найти географические координаты (широта и долгота) и высота надуровнем моря любого объекта или любой точки на географической карте Google.
Поиск географических координат (широта и долгота) по адресу.
Если вы хотите узнать GPS координаты любого здания
вам необходимо ввести в поисковое поле (Укажите aдрес) адрес этого места и нажать на кнопку
вам местоположение согласно вашему поисковому запросу и вы получите географические координаты точки
на карте мира (широта и долгота) в десятичных градусах и высота над уровнем моря в метрах.
DD — означает (десятичные градусы).
Вы сможете найти место на географической карте мира по DD (десятичные градусы), если у вас уже есть
географические координаты GPS в DD десятичные градусы, тогда введите их в соответствующие
поля (широта и долгота) и нажмите на кнопку поиска (Поиск места), на географической карте мира
вы увидите маркер и его положение будет соответствовать вашим GPS координатам в DD десятичные градусы.
DMS — означает (градусы, минуты, секунды).
Вы сможете найти место на географической карте мира по DMS (градусы, минуты, секунды), если у вас уже
есть географические координаты GPS в DMS градусы, минуты, секунды, тогда введите их в соответствующие
и нажмите на кнопку поиска (Поиск места), на географической карте мира вы увидите маркер и его положение
будет соответствовать вашим GPS координатам в DMS градусы, минуты, секунды.
Если вам нужно узнать географические GPS координаты любой точки на карте мира кликните левой кнопкой
компьютерной мыши на нужное место на географической карте мира и вы получите
географические GPS координаты (широта и долгота) этого места, высота
над уровнем моря в метрах, а также подробный адрес этой точки на карте мира.
Если вам понравился наш сервис определения GPS координат и вы считаете его полезным
для людей, пожалуйста поделитесь ссылкой с друзьями на наш сервис!
gps-coordinates.ru
Основы стереозрения / Habr
В данной статье содержатся базовые сведения о математическом аппарате, используемом в стерео зрении. Идея ее написания появилась после того как я начал работать с методами стерео зрения, в частности использовать алгоритмы реализованные в OpenCV. Эти алгоритмы зачастую ссылаются на различные понятия, такие как «фундаментальная матрица», «эпиполярная геометрия», «триангуляция». Существуют очень хорошие книжки по компьютерному зрению, в которых описывается, в том числе и стерео зрение и все необходимые понятия, но в них, нередко, бывает представлено слишком много информации для новичка. Здесь же, в краткой форме изложены базовые сведения о том, как работает стерео зрение и основные связанные с ним необходимые понятия:- проективная геометрия и однородные координаты
- модель камеры
- эпиполярная геометрия (epiporal geomerty), фундаментальная и существенная матрицы (fundamental matrix, essential matrix)
- триангуляция стереопары точек
- карта глубины(depth map), карта смещений(disparity map) и идея, лежащая в основе ее вычисления
Для понимания содержимого статьи достаточно иметь общее представление об аналитической геометрии и линейной алгебре: знать, что такое матрица, вектор, скалярное и векторное произведение.
В геометрии стерео зрения значительную роль играет проективная геометрия. К проективной геометрии есть несколько подходов: геометрический (подобно Евклидовой геометрии ввести понятие геометрических объектов, аксиом и из этого выводить все свойства проективного пространства), аналитический (рассматривать все в координатах, как в аналитическом подходе к Евклидовой геометрии), алгебраический.Для дальнейшего изложения в основном понадобиться понимание аналитического подхода к проективной геометрии, и именно он и изложен ниже.
Точки проективной плоскости. Рассмотрим двухмерное проективное пространство (которое еще называется проективной плоскостью). В то время как на обычной Евклидовой плоскости точки описываются парой координат (x,y)T, на проективной плоскости точки описываются трехкомпонентным вектором (x,y,w)T. При этом для любого ненулевого числа a, векторы (x,y,w)T и (ax, ay, aw)T соответствуют одной и той же точке. А нулевой вектор (0,0,0)T не соответствует никакой точке и выкидывается из рассмотрения. Такое описание точек плоскости называется однородными координатами (homogeneous coordinates).
Точкам проективной плоскости можно сопоставить точки обычной Евклидовой плоскости. Координатному вектору (x,y,w)T при w ≠ 0 сопоставим точку Евклидовой плоскости с координатами (x/w, y/w)T. Если же w = 0, т.е. координатный вектор имеет вид (x, y, 0T), то будем говорить, что эта точка в бесконечности. Таким образом, проективную плоскость можно рассматривать как Евклидовую плоскость, дополненную точками из бесконечности.
Перейти от однородных координат (x, y, w)T к обычным Евклидовым можно путем деления координатного вектора на последнюю компоненту и последующего ее отбрасывания (x,y,w)T → (x/w,y/w)T. А от Евклидовых координат (x,y)T перейти к однородным можно за счет дополнения координатного вектора единичкой: (x,y)T → (x,y,1)T
Прямые на проективной плоскости. Любая прямая на проективной плоскости описывается, подобно точке, трехкомпонентным вектором l = (a,b,c)T. Опять же вектор, описывающий прямую, определен с точностью до ненулевого множителя. При этом уравнение прямой будет иметь вид: lTx = 0.
В случае, когда a2 + b2 ≠ 0 мы имеем аналог обычной прямой ax + by + c = 0. А вектор (0,0,w) соответствует прямой лежащей в бесконечности.
Трехмерное проективное пространство. По аналогии с проективной плоскостью, точки трехмерного проективного пространства определяются четырехкомпонентным вектором однородных координат (x,y,z,w)T. Опять же для любого ненулевого числа a, координатные вектора (x,y,z,w)T и (ax,ay,az,aw)T соответствуют одной и той же точке.
Как в случае проективной плоскости, между точками трехмерного Евклидова пространства и трехмерного проективного пространства можно установить соответствие. Вектору однородных координат (x,y,z,w)T при w ≠ 0 соответствует точка Евклодова пространства с координатами (x/w,y/w,z/w)T. А про точку с вектором однородных координат вида (x,y,z,0)T говорят, что она лежит в бесконечности.
Проективное преобразование. Еще одна вещь, которая потребуется для дальнейшего изложения — это проективные преобразования (homography, projective transformation — в англ. литературе). С геометрической точки зрения, проективное преобразование — это обратимое преобразование проективной плоскости (или пространства), которое переводит прямые в прямые. В координатах, проективное преобразование выражается в виде невырожденной квадратной матрицы H, при этом координатный вектор x переходит в координатный вектор x‘ по следующей формуле: x‘ = H x.
Современные CCD-камеры хорошо описываются с помощью следующей модели, называемой проективной камерой (projective camera, pinhole camera). Проективная камера определяется центром камеры, главной осью — лучом начинающимся в центре камеры и направленным туда, куда камера смотрит, плоскостью изображения — плоскостью на которую выполняется проецирование точек, и системой координат на этой плоскости. В такой модели, произвольная точка пространства X проецируется на плоскость изображения в точку x лежащую на отрезке CX, который соединяет центр камеры C с исходной точкой X (см. рис. 1).
Рисунок 1: Модель камеры. C — центр камеры, Cp — главная ось камеры. Точка X трехмерного пространства проецируется в точку x — на плоскости изображения.
Формула проецирования имеет простую математическую запись в однородных координатах:
Матрица P выражается следующим образом P = KR[ I | —c] = K[R|t], где K — верхняя треугольная матрица внутренних параметров камеры размера 3 × 3 (конкретный вид приведен ниже), R — ортогональная матрица размера 3 × 3, определяющая поворот камеры относительно глобальной системы координат, I — единичная матрица размера 3 × 3, вектор c — координаты центра камеры, а t = −Rc.
Стоит отметить, что матрица камеры определена с точностью до постоянного ненулевого множителя, который не изменит результатов проецирования точек по формуле x = P X. Однако этот постоянный множитель обычно выбирается так, что бы матрица камеры имела вышеописанный вид.
В самом простейшем случае, когда центр камеры лежит в начале координат, главная ось камеры сонаправлена оси Cz, оси координат на плоскости камеры имеют одинаковый масштаб (что эквивалентно квадратным пикселям), а центр изображения имеет нулевые координаты, матрица камеры будет равна P = K[I|0], где
Помимо этого, в силу неидеальности оптики, на изображениях, полученных с камер, присутствуют искажения-дисторсии (distortion). Данные искажения имеют нелинейную математическую запись:
Дисторсии не зависят от расстояния до объекта, а зависят только от координат точек, в которые проецируются пиксели объекта. Соответственно для компенсации дисторсий обычно выполняется преобразование исходного изображения полученного с камеры. Это преобразование будет одним и тем же для всех изображений, полученных с камеры, при условии постоянства фокусного расстояния (математически — одной и той же матрицы внутренних параметров).
В ситуации, когда известны внутренние параметры камеры и коэффициенты дисторсии говорят, что камера откалибрована.
Об определении трехмерных координат наблюдаемых точек можно говорить, когда есть как минимум две камеры.Матрицы пары камер, калибровка. Пусть имеются две камеры, заданные своими матрицами P и P‘ в некоторой системе координат. В таком случае говорят, что имеется пара откалиброванных камер. Если центры камер не совпадают, то эту пару камер можно использовать для определения трехмерных координат наблюдаемых точек.
Зачастую, система координат выбирается так, что матрицы камер имеют вид P = K[I|0], P‘ = K‘[R‘|t‘]. Это всегда можно сделать, если выбрать начало координат совпадающее с центром первой камеры, и направить ось Z вдоль ее оптической оси.
Калибровка камер обычно выполняется, за счет многократной съемки некоторого калибровочного шаблона, на изображении можно легко выделить ключевые точки, для которых известны их относительные положения в пространстве. Далее составляются и решаются (приближенно) системы уравнений, связывающие координаты проекций, матрицы камер и положения точек шаблона в пространстве.
Существуют общедоступные реализации алгоритмов калибровки, например, Matlab Calibration toolbox. Так же библиотека OpenCV включает в себя алгоритмы калибровки камер и поиска калибровочного шаблона на изображении.
Эпиполярная геометрия. Перед тем как перейти к описанию собственно метода вычисления трехмерных координат точек, я опишу некоторые важные геометрические свойства, связывающие положения проекций точки трехмерного пространства на изображениях с обеих камер.
Пусть имеются две камеры, как изображено на рисунке 2. C — центр первой камеры, C‘ — центр второй камеры. Точка пространства X проецируется в x на плоскость изображения левой камеры и в x‘ на плоскость изображения правой камеры. Прообразом точки x на изображении левой камеры является луч xX. Этот луч проецируется на плоскость второй камеры в прямую l‘, называемую эпиполярной линией. Образ точки X на плоскости изображения второй камеры обязательно лежит на эпиполярной линии l‘.
Рисунок 2: Эпиполярная геометрия
Таким образом, каждой точке x на изображении левой камеры соответствует эпиполярная линия l‘ на изображении правой камеры. При этом пара для x на изображении правой камеры может лежать только на соответствующей эпиполярной линии. Аналогично, каждой точке x‘ на правом изображении соответствует эпиполярная линия l на левом.
Эпиполярную геометрию используют для поиска стереопар, и для проверки того, что пара точек может быть стереопарой (т.е. проекцией некоторой точки пространства).
Эпиполярная геометрия имеет очень простую запись в координатах. Пусть имеется пара откалиброванных камер, и пусть x — однородные координаты точки на изображении одной камеры, а x‘ — на изображении второй. Существует такая матрица F размера 3 × 3, что пара точек x, x‘ является стереопарой тогда и только тогда, когда:
В случае, когда матрицы камер имеют вид P = K[I|0], P‘ = K‘[R|t] фундаментальная матрица может быть вычислена по формуле:
С помощью фундаментальной матрицы вычисляются уравнения эпиполярных линий. Для точки x, вектор, задающий эпиполярную линию, будет иметь вид l‘ = F x, а уравнение самой эпиполярной линии: l‘Tx‘ = 0. Аналогично для точки x‘, вектор, задающий эпиполярную линию, будет иметь вид l = FTx‘.
Помимо фундаментальной матрицы, существует еще такое понятие, как существенная матрица (essential matrix): E = K‘TF K. В случае, когда матрицы внутренних параметров будут единичными существенная матрица будет совпадать с фундаментальной. По существенной матрице можно восстановить положение и поворот второй камеры относительно первой, поэтому она используется в задачах, в которых нужно определить движение камеры.
Триангуляция точек (triangulation). Теперь собственно перейдем к тому, как определить трехмерные координаты точки по координатам ее проекций. Этот процесс в литературе называется триангуляцией.
Пусть имеются две откалиброванные камеры с матрицами P1 и P2. x1 и x2 — однородные координаты проекций некоторой точки пространства X. Тогда можно составить следующую систему уравнений:
Идея, лежащая в основе построения карты глубины по стереопаре очень проста. Для каждой точки на одном изображении выполняется поиск парной ей точки на другом изображении. А по паре соответствующих точек можно выполнить триангуляцию и определить координаты их прообраза в трехмерном пространстве. Зная трехмерные координаты прообраза, глубина вычисляется, как расстояние до плоскости камеры.
Парную точку нужно искать на эпиполярной линии. Соответственно, для упрощения поиска, изображения выравнивают так, что бы все эпиполярные линии были параллельны сторонам изображения (обычно горизонтальны). Более того, изображения выравнивают так, что бы для точки с координатами (x0, y0) соответствующая ей эпиполярная линия задавалась уравнением x = x0, тогда для каждой точки соответствующую ей парную точку нужно искать в той-же строчке на изображении со второй камеры. Такой процесс выравнивания изображений называют ректификацией (rectification). Обычно ректификацию совершают путем ремеппинга изображения и ее совмещают с избавлением от дисторсий. Пример ректифицированных изображений приведен на рисунке 3, картинки взяты из базы изображений сравнения различных методов построения карты глубины http://vision.middlebury.edu/stereo.
После того как изображения ректифицированы, выполняют поиск соответствующих пар точек. Самый простой способ проиллюстрирован на картинке 4 и состоит в следующем. Для каждого пикселя левой картинки с координатами (x0, y0) выполняется поиск пикселя на правой картинке. При этом предполагается, что пиксель на правой картинке должен иметь координаты (x0 — d, y0), где d — величина называемая несоответствие/смещение (disparity). Поиск соответствующего пикселя выполняется путем вычисления максимума функции отклика, в качестве которой может выступать, например, корреляция окрестностей пикселей. В результате получается карта смещений (disparity map), пример которой приведен на рис. 3.
Рисунок 3: Пример ректифицированных картинок, и соответствующей им disparity map.
Собственно значения глубины обратно пропорциональны величине смещения пикселей. Если использовать обозначения с левой половины рисунка 4, то зависимость между disparity и глубиной можно выразить следующим способом:
Рисунок 4: Вычисление карты глубины.
Из-за обратной зависимости глубины и смещения, разрешающая способность систем стерео зрения, которые работают на основе данного метода, лучше на близких расстояниях, и хуже на далеких.
habr.com
Определение, передача координат телефоном и поиск места по ним.
В современном мире продолжают теряться и гибнуть в лесах люди с заряженным мобильным телефоном. Люди ЗВОНЯТ спасателям с просьбой их найти, имея в кармане по сути GPS приемник — цирк. Liza Alert всячески ратует за возможность выдавать данные позиционирования смартфона при поисках, но кто-ж им даст.
На мой взгляд надо действовать маспросветом — объяснять людям, что их устройство в кармане может определять координаты, передавать их и показывать место на карте по полученным координатам.
Статья пригодится не только желающим быть спасенными и спасать, но и всем, кто хочет пересылать координаты чего угодно. От вашего лагеря в лесу, до места парковки машины. Я учу этому каждого участника своих походов.
Содержание:
Основной затык у народонаселения в этом вопросе из-за убежденности, что координаты определяются благодаря интернету. Это не так. Почему никого не смущает, что GPS во всю использовался в 1980-х, а мобильный интернет появился, сами знаете когда? О том как работает GPS, и о том какой навигатор выбрать у меня есть отдельная статья.
Если вы не понимаете, что такое координаты, почему они в градусах измеряются, откуда считаются и т.д. рекомендую прочитать эту статью — полезно для понимания.
Получение координат
Для начала надо включить Геопозиционирование (GPS) в вашем телефоне. Обычно оно находится в шторке сверху.
Затем запускаем программу для навигации. Я расскажу на примере Google Maps, Яндекс Карт, Maps.me и Locus Map. Точность от приложения не зависит — все программы запрашивают данные о местоположении у операционной системы.
Если GPS давно не включался, то телефону потребуется некоторое время, чтобы поймать сигнал спутников. Как только это произойдет, диаметр кружочка, обозначающего ваше местоположение сузится до примерно метров 10 — этого достаточно, чтобы вас найти.

Если вам нужны координаты не вашего местоположения, а какого-то другого места на карте, то GPS включать вообще не нужно. GPS нужен только для позиционирования.
У всех на Андроид установлены по умолчанию Google карты. Начнём с них. Всё просто: жмем и удерживаем на том месте карты, координаты которого мы хотим узнать. Приложение мне покажет вот такую картинку:

Обратите внимание, что вверху приложение показало координаты в формате «градусы, доли градуса». Сначала широту, а потом долготу. Это десятичная дробь, целая часть от дробной отделена точкой, а широта от долготы запятой.

В этом формате даже ушли от обозначения сторон света буквами (NSWE). Для широты положительные значения — это северное полушарие, отрицательные — южное. Для долготы положительные значения — восточное полушарие, а отрицательные — западное. Т.е. координаты Лос-Анджелеса в этом формате будут: 34.05266, -118.25684, а Рио-де-Жанейро -22.89768, -43.28613.
Внизу приложение Google Карт показало мне координаты того же самого места, но в другом формате «градусы, минуты, секунды, десятичные доли секунд». Он менее удобен как для диктовки по телефону или радиостанции, так и для печати на клавиатуре компьютера. Единственный гипотетический случай, когда вам пригодятся координаты в таком формате — это когда у адресата сообщения нет интернета, а есть бумажная карта с координатной сеткой по краям, — тогда он сможет найти указанное место.
Если бы в момент создания этого скриншота у меня был бы интернет, то приложение показало бы мне не координаты, а название объекта в этом месте. Например адрес дома или название магазина.
Нажмите два раза на координаты вверху экрана, скопируйте их и отправляйте в обычном SMS или мессенджере, если ловит интернет.
В остальных программах все происходит аналогичным образом.
В Яндекс Картах надо тапнуть на любом месте экрана и в появившимся внизу меню нажать «Что здесь».
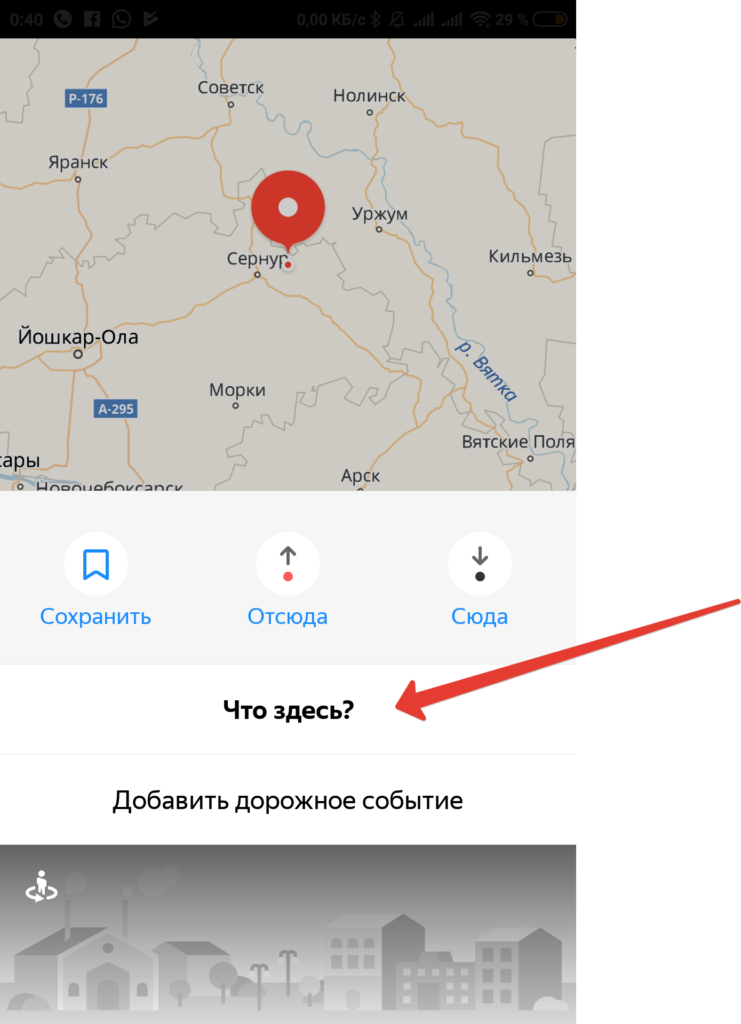
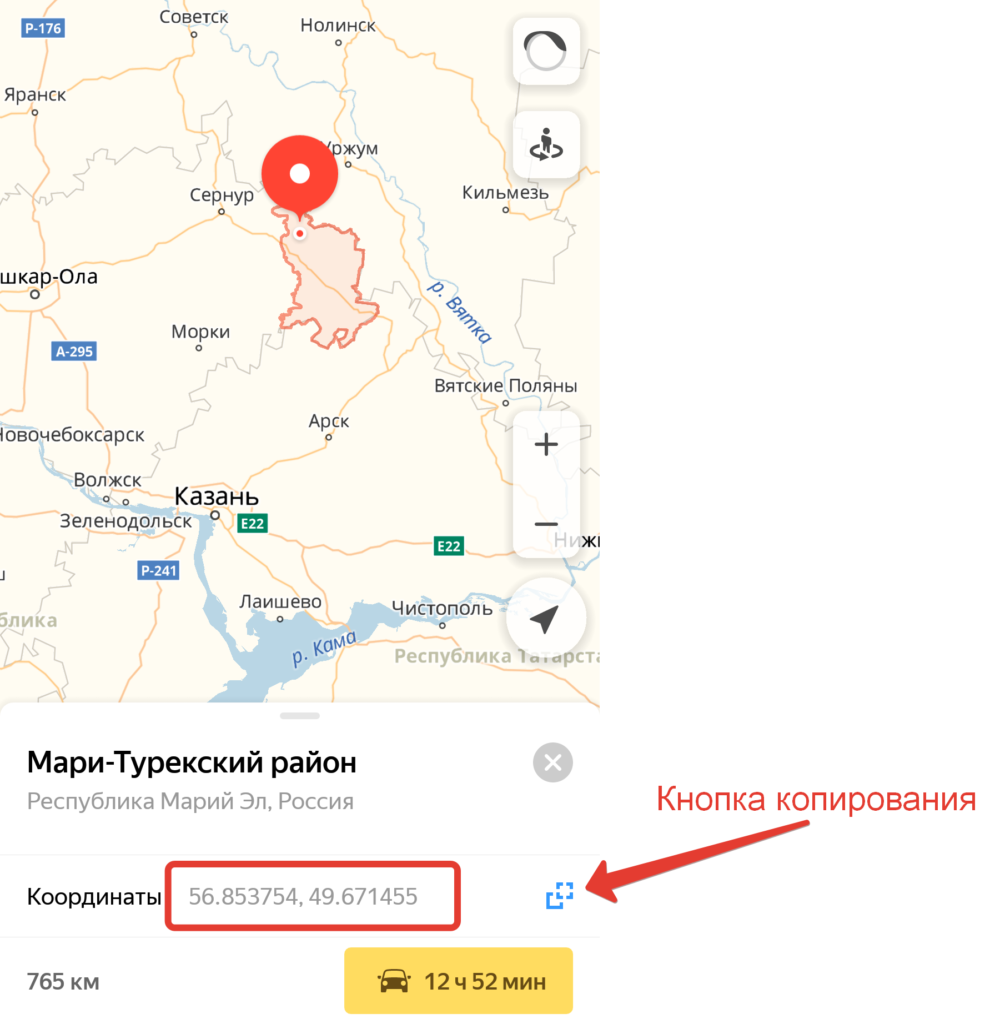
Огромный минус приложения Я.Карт в том что координаты они показывают только есть на телефоне есть интернет или карта региона заранее скачана на телефон.
Лучше всего пользоваться Maps.me.
Во-первых, они, как и приложение гуглкарт, показывают координаты по всему миру, даже если карта нужного региона не скачана.
Во-вторых, если карту скачать, они используют OSM в котором, в отличие от Яндекс и Гугл карт, есть тропинки в лесах и всякая ненаселенка (хоть именно в maps.me её и мало). Т.е. верней помогут выбраться из леса.
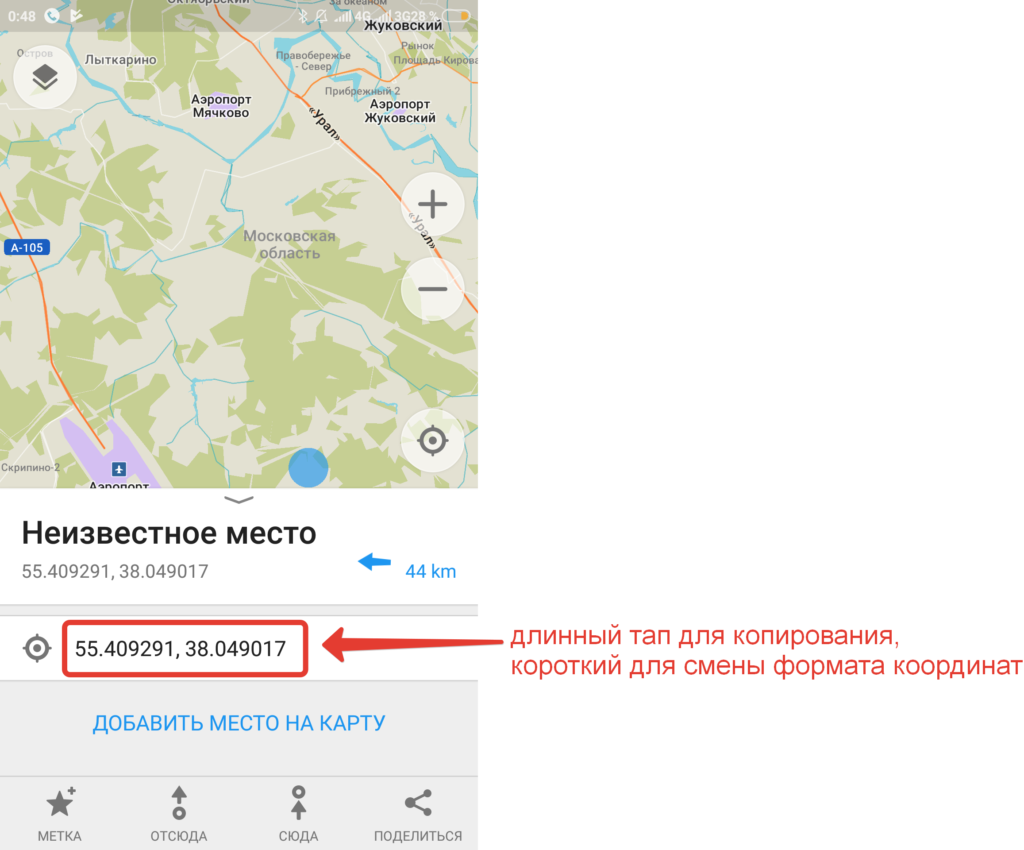
Также жмем и удерживаем на интересующем месте. Появившуюся шторку внизу тянем вверх.

Появятся координаты
В приложении Locus Map, если он настроен по моей инструкции, проще всего поместить интересующее место в центр экрана (под крестик) и тапнуть на координаты вверху слева — это действие копирует координаты в буфер обмена. В приложении можно использовать и сохранять в офлайн любые, в том числе и растровые карты, хоть тот же генштаб.

Если у вас настроено меню по другому, то координаты любого места на карте можно получить так:
Длинный тап на нужном месте карты, появится меню. Жмем на описание места (обвел в красную рамку)
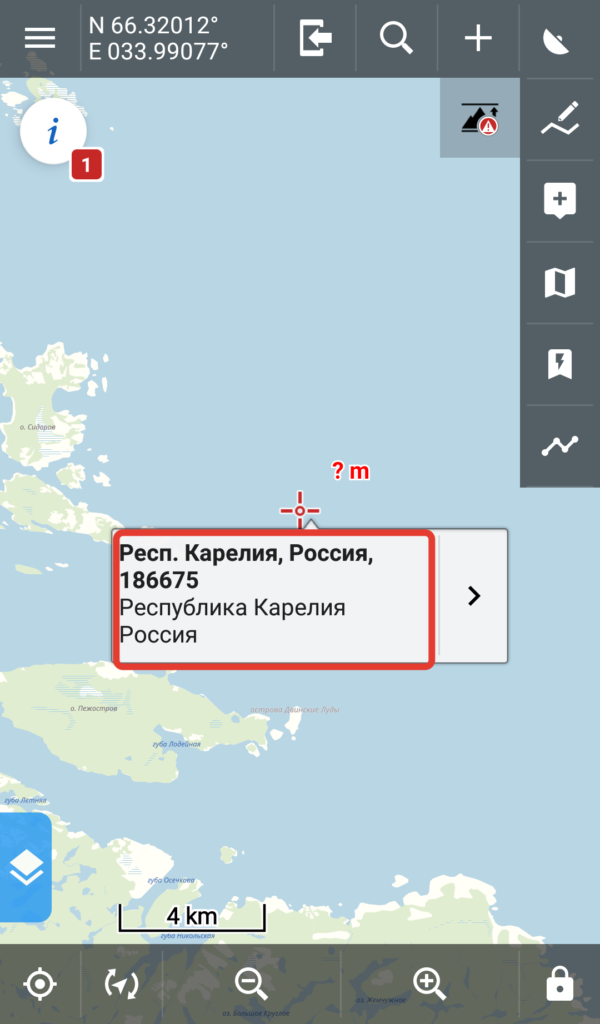
Откроется информация о точке. Жмем на координаты — это скопирует их в буфер обмена.
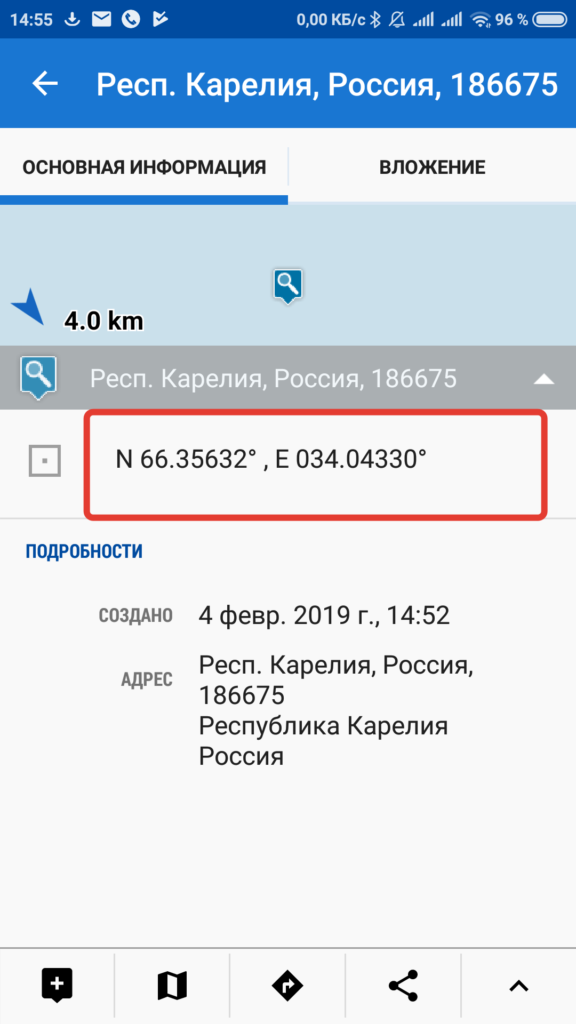
Отправка координат
Скопированные координаты отправляйте в обычном SMS или мессенджере, если ловит интернет.
Обратите внимание на то, как вы отправляете координаты. В современных телефонах часто скопировать текст всего сообщения быстрей и удобней, чем часть сообщения (длинный тап копирует всё сообщение, а часть текста надо выбирать ползунками). Потому из соображений оперативности и уважения к собеседнику лучше отправлять координаты одним сообщением, а пояснения к ним — другим. Адресат увидит в любом случае ваши сообщения, а скопировать координаты ему будет проще.
Если сложилась такая ситуация, что надо передать координаты голосом (по радиостанции), удостоверьтесь, что вы работаете в одном и том же формате координат. Имейте ввиду, что люди часто вообще не знают, что такое эти палочки над цифрами (например: N 43°51′58.38″ E 32°17′59.30″), и что они обозначают минуты и секунды широты и долготы. Поэтому лучше использовать формат «градусы, доли градусов» (55.75185 37.79297 или N 55.75185° E 37.79297°) — там только один знак, разделяющий целую и дробную часть градуса.
Также не подготовленный пользователь, записывающий координаты в неизвестный вам прибор, может путать куда писать цифры обозначающие сотни и десятки. Например максимальное значение долготы 180 градусов, т.е в поле записи будет три ячейки для цифр. Неофит легко может записать долготу Москвы не как 037 градусов восточной долготы, а как 370. При применении форматов записи координат где есть десятки или сотни минут и секунд путаница возрастает в разы. Это еще одна причина использовать формат «градусы, доли градусов». Это всем знакомая десятичная дробь. Количество знаков после запятой может быть разным (обычно 5 или 6), но пропущенный последний шестой знак не критично повлияет на точность. Обычному человеку хватит и четырех знаков. (6й знак уточняет позицию на 8 см на экваторе, а в остальных местах еще меньше, а 5й знак 80 см на экваторе. В наших широтах — 64 см). При этом для той же точности в других форматах записи надо использовать большее количество знаков.
Что делать с этим дальше?
Поиск по координатам
Предположим вы получили SMS с координатами и просьбой о помощи.
Просто вставьте полученные координаты в строку поиска в одном из перечисленных выше приложений. Опять таки Google maps, Maps.me покажут вам координаты даже если нету интернета, а Яндекс карты нет (Якарты покажут, только если вы скачали заранее карту того региона).
Locus Map по умолчанию, при нажатии на кнопку поиска (лупу) открывает окно поиска с помощью того же поисковика Google, т.е работает через интернет. Если его нет, надо просто открыть окно поиска по координатам.
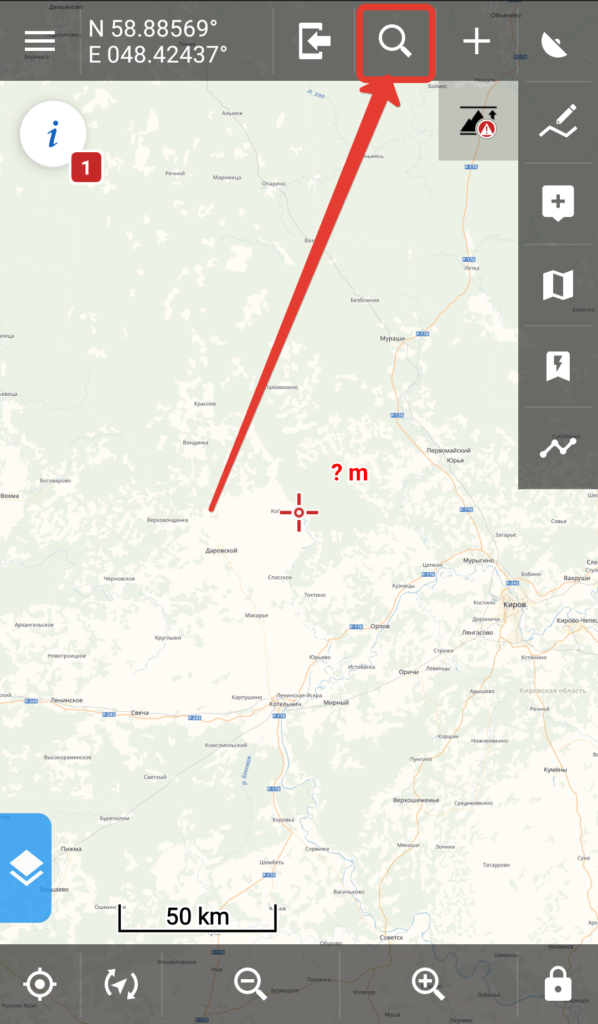
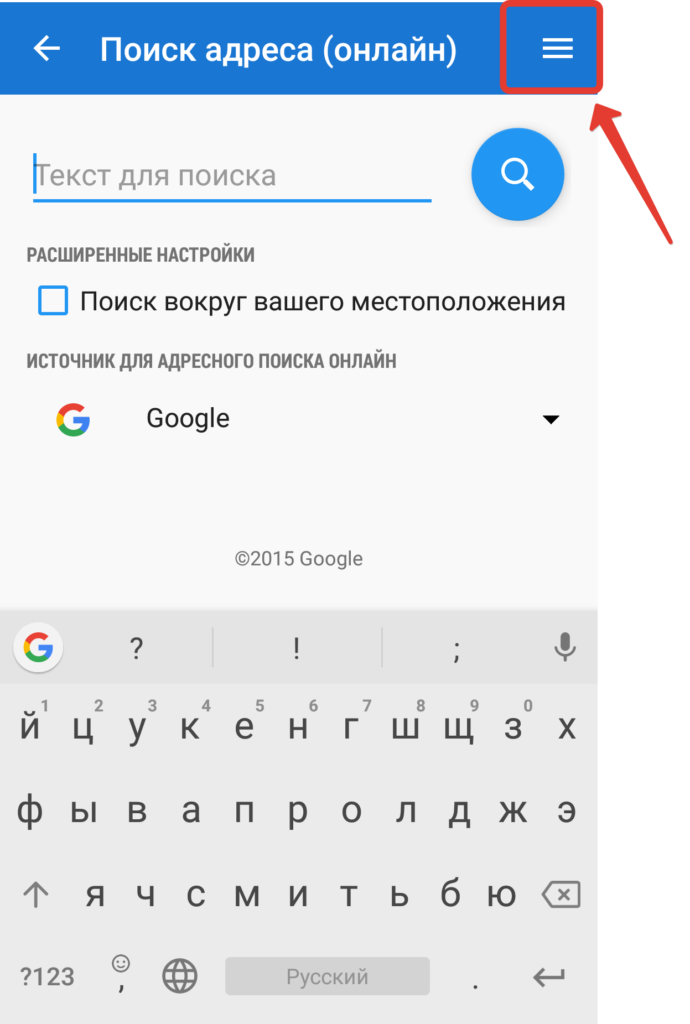
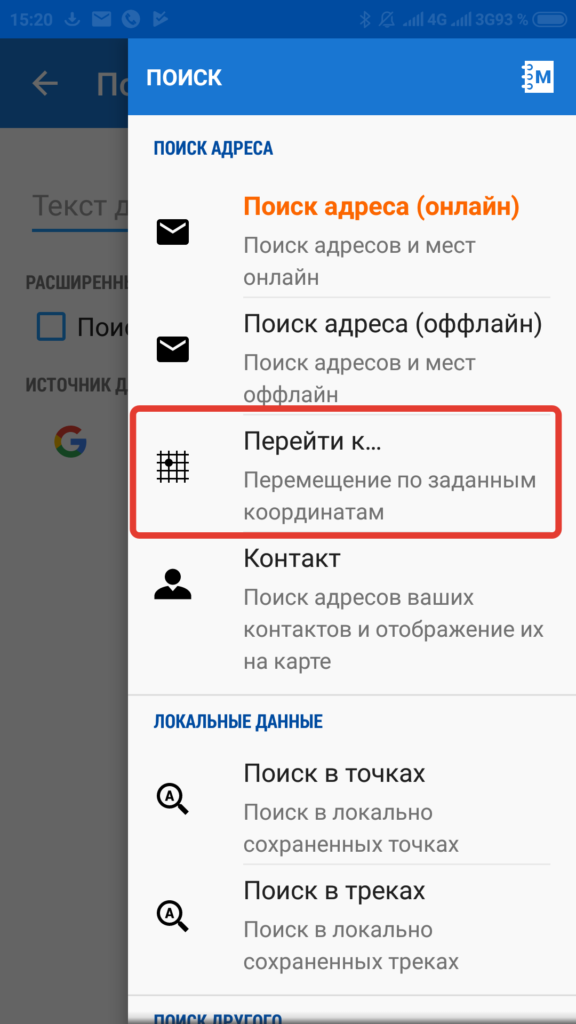
Тут можно выбрать вставить ранее скопированные координаты из буфера обмена или ввести их вручную (если их например голосом диктуют).

Если мы выбрали вставку координат из памяти, то откроется такое вот окно. Останется только нажать ОК.
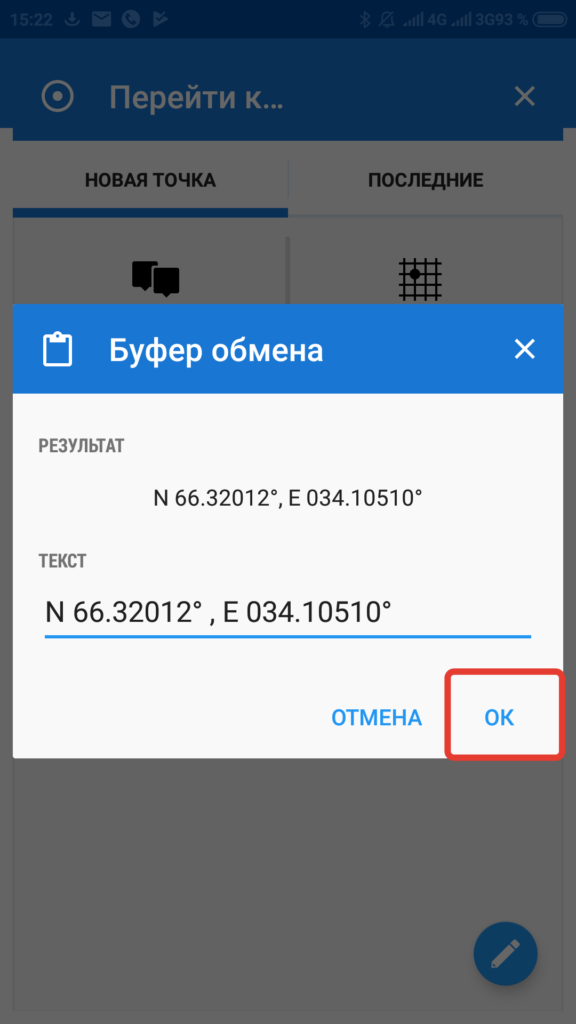
Если выберем ручной ввод координат, то откроется вот такое окно. Можно выбрать формат записи координат.
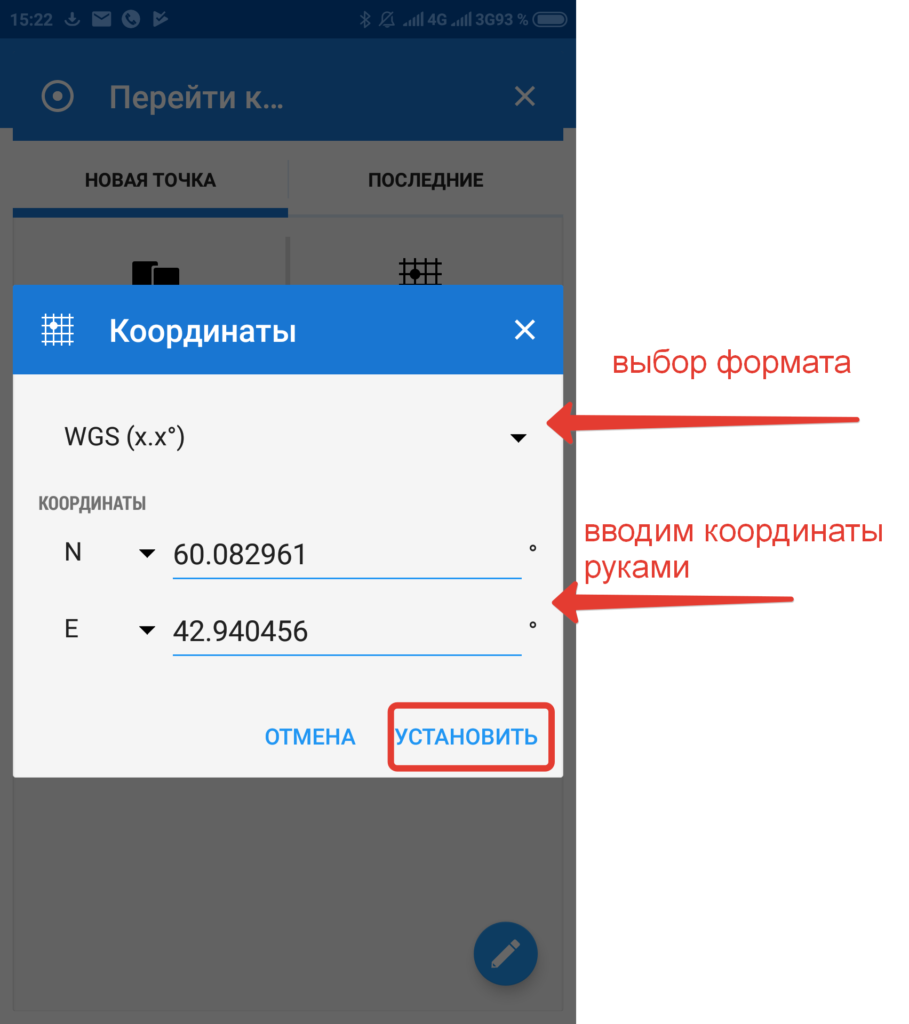
В итоге приложение покажет на экране точку с заданными вами координатами.
Про поиск места по координатам с экрана компьютера расскажу в другой статье.
Компас в телефоне. Определение направления.
Если вы потерялись в лесу, аккумулятор телефона у вас вполне себе полон, алгоритм действий прост:
- Включаем GPS
- Открываем картографическое приложение, смотрим куда проще выйти в цивилизацию.
- Определяем направление движения на местности
- Начинаем движение, периодически сверяясь с навигатором.
- ….
- Profit!
Когда мы движемся навигатор, исходя из изменения наших координат, понимает в какую сторону мы двигаемся и даже начинает рисовать нас не как точку, а как стрелочку (вспомните любой автомобильный навигатор), указывающую направление нашего движения.
Если батарея телефона на исходе, то (Капитан очевидность намекает) для её экономии включать навигатор с GPS надо изредка, для корректировки пути. В этом случае весьма полезным будет научится пользоваться компасом в телефоне — вы стразу поймете направление, и не надо будет проходить лишние десятки метров с включенным GPS, чтобы понять направление движения.
Практически любой современный смартфон оборудован компасом — надо только поставить приложение. Одно из самых простых GPS Status & Toolbox. А вот например экран компаса в приложении Locus Map.
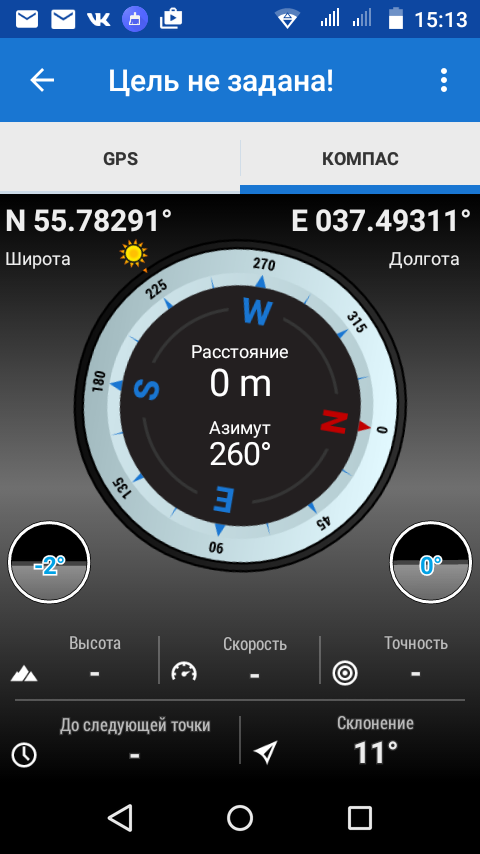
Ввиду того, что на компас в электронике электромагнитное излучение оказывает особое влияние, для корректной работы компасов в таких приборах надо проводить их калибровку, причем чем чаще, тем лучше. В продукции Garmin надо в меню компаса выбрать пункт «Калибровать компас» и следовать инструкциям на экране (Программа покажет как покрутить прибор в разных плоскостях). Чтобы откалибровать компас на Android, надо или так же выбрать соответствующий пункт в меню приложения, или, если он отсутствует, запустить компас, а потом делать телефоном вот такие движения.
Отдельная статья по навигацию с компасом у меня тут. А вот статья как ориентироваться по сторонам света, если у вас ни компаса, ни GPS.
shuriktravel.ru
Привязка географической информации к фотографиям

Идея записывать вместе с каждой фотографией координаты точки, в которой они сделаны, возникла еще на заре цифровой фотографии и была почти сразу реализована. Сегодня эта идея пришла в массы и обросла множеством сервисов. С самого начала возникла и сегодня продолжается реализация идеи на аппаратном уровне, когда GPS приемник прямо связывается с камерой, либо он в нее встроен, либо подсоединен к ней через последовательный порт, либо установлен на камеру и получает сигнал о том, что сделан снимок, от синхроконтакта вспышки. Sony выпустила также устройство GPS-CS1, которое записывает просто координаты каждые 15 с, а потом они синхронизуются по времени со сделанными снимками, и информация о координатах записывается в файле. Учитывая, что сегодня и GPS приемники, и камеры стали весьма распространенными и в повседневной жизни, возможно, вам и не придется покупать дополнительное устройство, можно воспользоваться уже имеющимся у вас GPS приемником и камерой, остается только привязать данные о координатах к конкретным снимкам. Раньше было существенное ограничение, связанное с тем, что память GPS навигатора переполнялась, и приходилось каждый день скачивать информацию в компьютер. Если вы снимали редко, а GPS использовался в навигации, то вполне вероятно, что, приехав из похода, вы сможете извлечь информацию только о последнем дне. Сейчас, когда у GPS навигаторов появилась возможность записывать пройденные пути на карты памяти, вопрос ее нехватки практически полностью снят. В Интернете можно найти несколько десятков программ, предназначенных для привязки фотографий к координатам. Более менее полный список можно найти здесь и здесь. Среди них есть и коммерческие, но большинство бесплатные и даже с открытыми исходными кодами. Я попытался попробовать многие их них, однако если по каким-то причинам программа сразу не начинала работать корректно, то я не пытался разобраться, а сразу переходил к следующей. Поэтому весьма вероятно, что среди тех программ, которые я отбраковал, есть и достойные, которые на другой конфигурации оборудования начнут работать сразу и без проблем. Коммерческие программы я тоже не рассматривал, поскольку их демонстрационные версии вносят умышленную ошибку около километра, и мне показалось неразумным тратить на них время при наличии большого количества открытых программ.
Кроме того, число рассматриваемых программ сократилось, поскольку у меня были достаточно специфические дополнительные требования. А именно: для записи координат использовался навигатор Etrex Venture Cx, который сохраняет данные о координатах в формате GPX (GPS Exchange Format). Формат стандартный, но выясняется, что фирма Garmin и некоторые создатели программ этот стандарт понимают по-разному. К счастью, есть универсальные программы, преобразующие один формат в другой. И среди них я бы выделил GPSBabel. В частности, в этой программе можно попросить преобразовать формат GPX, взятый из навигатора Garmin, в тот же самый формат, но результат этого преобразования будут понимать уже все программы.
Второе требование состояло в том, что мне хотелось сразу привязать фотографии в формате RAW, чтобы все полученные из исходных фотографии были уже с помеченными координатами, и не надо было бы снова определять координаты по времени, когда сделан снимок. Потому что с временем, как оказалось, существует довольно много проблем. И если их еще умножить тем, что преобразованные файлы сделаны и обработаны в разное время, и исходная информация времен снимка может быть потеряна или через некоторое время вы не сможете вспомнить, в каком часовом поясе вы снимали. Многие из рассмотренных мной программ имеют довольно изощренные настройки для коррекции возможных проблем с установкой времен. Тем не менее, лучше сразу настроить навигатор и камеру таким образом, чтобы этих проблем не возникало. У моего навигатора есть возможность выбрать способ записи трека — автоматический или через заданный интервал времени. В автоматическом режиме, если вы быстро перемещаетесь, то точек пишется много, если же стоите на месте, то они вообще не пишутся. Это позволяет получить запись пути одинаково качественно, передвигаетесь ли вы пешком, или едете на машине. Однако если вы долго снимаете с одной точки, то может создаться ситуация, когда в момент съемки GPS навигатор не записал координаты, поскольку они не отличались от записанных полчаса назад. Во многих программах можно задать интервал времени, в котором координаты считаются совпадающими со сделанным снимком. Однако отсутствие информации может означать не только то, что вы не перемещались, но и то, что сигнал от спутника был потерян. В этом случае, если интервал достаточно большой, то снимку могут быть приписаны координаты, существенно отличающиеся от истинных. Поэтому я рекомендую установить запись по времени с интервалом в 10 с. Если вы снимаете не из окна автобуса, то точность будет более чем достаточна.
Следующая глобальная проблема — это какое время устанавливать в камере. Если вы путешествуете, или делаете снимки осенью или весной, когда могут перевести время, то устанавливать в камере местное время мне кажется плохой идеей, тем более, что идея местного времени сегодня полностью дискредитирована. Солнце в зените над моим домом в Москве летом в 13 часов 15 минут. Сегодня средства транспорта позволяют перемещаться на многие тысячи километров, и разумнее использовать единое мировое время, а не объяснять, по какому времени и с учетом какого временного периода вы договаривались о встрече. Навигатор ведет протокол по времени UTC (Coordinated Universal Time). Поэтому это же время имеет смысл и выставить на камере и никогда не менять вне зависимости от переездов или времени года. Учитывая, что я записываю координаты с интервалом в 10 с, я предпочитаю называть это время по старинке GMT (Greenvich Meridium Time). Этот вариант более информативен, поскольку означает, что отсчет ведется от местного времени на меридиане Гринвича и при заданной мной точности не отличается от UTC. Зная свои собственные координаты и это время, вы всегда легко можете вычислить, когда же у вас солнце будет в наивысшей точке, то есть местный полдень. Вся эта информация для фотографа отнюдь не бесполезная, поскольку позволяет представить, откуда и куда будет падать свет в предполагаемой точке съемки. Все беды от наук, поэтому, вероятно, люди, обозвавшие утро полднем, стремились побыстрее отправить всех, кто учил в школе географию, в сумасшедший дом.
Итак, если у нас камера и навигатор установлены по единому времени, то в дальнейшем можно игнорировать настройки Часовой пояс. Программы привязки фотографии к координатам
GPicSync
Для начальной пакетной обработки снятых фотографий я выбрал программу GPicSync.
Спартанский графический интерфейс, работа только с папками, просмотр только JPEG, но свою задачу она выполняет и достаточно быстро. Отмечу, что есть довольно много программ, работающих из командной строки, которые могут поспорить с данной по аскетизму, но я не люблю работать с клавиатурой 🙂 Программа использует EXIFTool и GPSbabel. Распространяется по лицензии GPL. Есть версии для Windows и Linux. Поддерживается русский язык.
Работает она сразу с папками, позволяет пакетно преобразовывать сразу много фотографий, работает с RAW, понимает файлы GPX от Garmin, записывает координаты в EXIF, позволяет добавлять автоматически в ключевые слова IPTC ближайшие географические названия, которые она берет из баз данных в Интернете. Кроме того, что она записывает информацию о координатах в файлы фотографий, она также создает файл в формате KML или KMZ.
KML (Keyhole Markup Language — язык разметки Keyhole) — язык разметки на основе XML, служащий для представления трехмерных геопространственных данных в программе Google Earth, которая носила название «Keyhole» до её приобретения компанией Google. KMZ являются результатом сжатия KML-файлов ZIP-способом. Подробнее см здесь.
Программа Google Earth распространяется бесплатно здесь.
Если вы хотите в походных условиях (без быстрого интернета) сориентироваться, где же вы сделали снимки, их надо нанести на какую-нибудь карту, которая сохранена у вас в ноутбуке. Для этого можно воспользоваться вышеупомянутой программой GPS Babel и преобразовать в формат WPT для просмотра в программе OziExplorer или снова в формат GPX, но уже с включенными в него путевыми точками, отмечающими сделанные снимки, для просмотра в программе MapSource, т. е. нанести фотографии на ту самую карту, по которой вы ориентировались, когда пользовались своим GPS навигатором.
Geotag
Для работы с отдельными фотографиями может оказаться хорошим выбором программа Geotag.
Эта программа написана на Java и, как следствие, одинаково легко запускается без переустановки и под Windows, и под Linux. Кроме того, она распространяется по лицензии GNU General Public License. Программа может все: работать с RAW файлами; просматривать их; записывать координаты в EXIF; просматривать положение фотографий на спутниковых снимках через программу Google Earth; добавлять географические названия в ключевые слова, пользуясь информацией с сайта GeoNames. Чтобы добиться такой универсальности, программа использует внешние модули сторонних разработчиков, которые надо устанавливать отдельно: ExifTool by Phil Harvey, GPSBabel, dcraw by Dave Coffin.
Программа позволяет экспортировать фотографии не только в Google Earth, но и, не устанавливая дополнительных программ, контролировать положение точки съемки через maps.google.com.
Из минусов этой программы надо отметить, что она очень медленная, т. е. на подготовку просмотра фотографии в формате RAW может уйти около минуты, и без конвертации не понимает файлы Garmin. Программа GPSBabel используется для связи с GPS приемником а для конвертации файлов ее надо запускать отдельно. Некоторые географические названия могут быть вставлены кириллицей, что можно было бы только приветствовать, но некоторые программы просмотра отказываются работать с такими файлами 🙁
Программа очень часто обновляется, так что есть надежда, что она будет совершенствоваться 🙂
COPIKS PhotoMapper
Если работать только с файлами в формате JPEG и только под Windows, то неплохим выбором будет программа COPIKS PhotoMapper.
Она же весьма эффективно справляется с задачей упаковки ранее привязанных к координатам фотографий в формат KMZ. Можно посмотреть, как это выглядит, скачав файл в 500 КБ.
Locr GPS Photo
Для последующей обработки и размещения фотографий в интернете может быть полезной программа Locr GPS Photo.
Удобна она и тем, что позволяет накладывать фотографии на космические снимки и карты, предоставленные разными компаниями. Можно выбирать между Google, Microsoft и YAHOO.
Привязывать фотографии с ее помощью я так и не научился, поскольку не нашел способа преобразовать GPX в приемлемый для нее формат NMEA. Поэтому для меня ее основное предназначение размещать фотографии в интернете. Это не единственная служба которая предоставляет подобную услугу, можно размещать фотографии в интернете и на сайте Panoramio.
Panorado Flyer
Удобным дополнением оказалась программа Panorado Flyer, которая позволяет редактировать координаты вручную, находить точку съемки в программе Google Earth по данным, записанным в EXIF, а также проводить обратную операцию — записывать координаты найденной на космическом снимке точки съемки в EXIF.
P.S.За последний год идея получила бурную поддержку в массах, и скоро любую точку земной поверхности можно будет увидеть не только из космоса, но и с уровня земли. Включив в Google Earth слой «География в интернете/Panoramio», вы увидите, что земля буквально усыпана пометками точек съемки, щелкнув по которым, можно увидеть фотографию.
www.ixbt.com
