Что такое расстояние от точки до точки – определение и примеры нахождения, метод координат расстояние от точки до прямой — Stoppanic

Содержание

формулы, примеры, решения, формула расстояния между двумя точками

В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.

Определение 1

Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.

Расстояние между точками на координатной прямой

Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.

В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.

К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.

Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднит

zaochnik.com

Задачи на расстояние от точки до кривой. Видеоурок. Алгебра 10 Класс

Тема: Производная

Урок: Задачи на расстояние от точки до кривой

Что такое расстояние от точки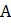 докривой? Точку 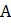можно соединить со многими точками кривой. Каждый раз будут получаться разные расстояния. Среди них нужно найти наименьшее. Это расстояние и будет называться расстоянием от точки до кривой. На кривой надо найти такую точку 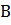, чтобы расстояние было наименьшим (см. рис. 1).

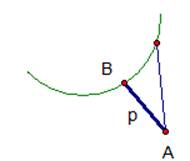
Рис. 1. Расстояние от точки до кривой.

Видим, что задача на расстояние – это задача на экстремум, на минимум, то есть без производной не обойтись.

Вспомним, что расстояние от точки до прямой – это длина перпендикуляра (см. рис.2).

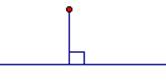
Рис. 2. Расстояние от точки до прямой.

Расстояние между прямыми – это тоже длина перпендикуляра (см. рис.3).

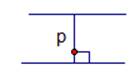
Рис. 3. Расстояние между прямыми.

Расстояние от точки до окружности легко найти. Нужно соединить центр с точкой

, в результате получится точка

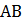– искомое расстояние (см. рис.4).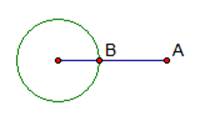

Рис. 4. Расстояние от точки до окружности.

Расстояние между двумя окружностями, которые не пересекаются. Нужно соединить центры, получим две точк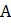и и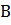

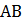– искомое расстояние (см. рис.5).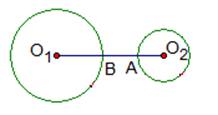

Рис. 5. Расстояние между двумя окружностями.

Сформулируем задачу в общем виде и напомним, каким образом ее решать. Мы повторили, что такое расстояние. Вспомним формулу расстояния между двумя заданными точками. Предположим, что на координатной плоскости даны две точк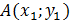и и 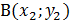(см. рис.6).

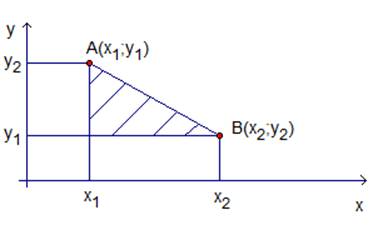
Рис. 6. Расстояние между двумя заданными точками.

Расстояние между точками вычисляется по формуле

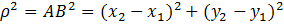Таким образом, находится расстояние между точками, если известны координаты этих точек.

На параболе 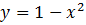найти точки ближайшие к началу координат, то есть к точке .

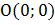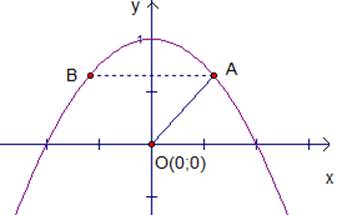
Рис. 7. График функции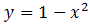

Решение.

Из простейшего анализа задачи можно увидеть, что задача имеет два решения, в силу симметрии графика функции относительно оси Y (см. рис.7).

Координаты искомой точки: 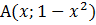. По соответствующей формуле можем найти квадрат расстояния:

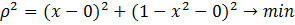. Это расстояние должно быть наименьшим. Упростим эту формулу и получим:

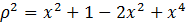или

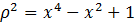Можно сразу использовать производную для решения задачи, но пока попытаемся воспользуемся свойствами биквадратной функции. С помощью замены переменной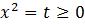

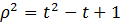, получим:

. Задача свелась к нахождению минимума следующей квадратичной функции 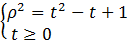. Найдем абсциссу вершины 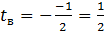(см. рис.8).

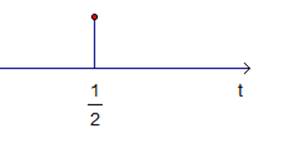
Рис. 8. Абсцисса вершины параболы.

Задача практически решена. Наименьшее значение этой функции будет тогда, когда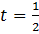

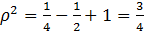. Вычислим

. Значит, функция

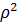ведет себя следующим образом (см. рис.9):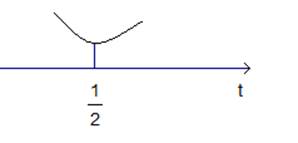

Рис. 9. Схематический график функции .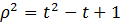

Без производной, с помощью свойств квадратичной функции, решили задачу. Если 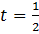, то

, отсюда

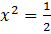
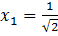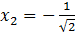. Если значения координат

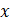известны, вычислим значения

;

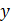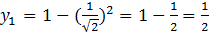Получили ответ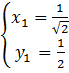

;

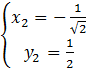Итак, была задача: найти точки на кривой, которые бы отстояли от начала координат на наименьшее расстояние. Такие точки найдены. Первая точка — 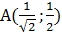, вторая точка – .

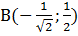Напомним ход решения задачи. Точка 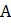зависит только от 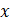, ее координаты – 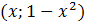. При выражении квадрата расстояния, получили функцию от 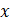. Можно с помощью производной найти минимум. Можно сделать проще. Если сделать замену 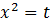, получим квадратичную функцию и можно найти наименьшее значение данной квадратичной функции.

Ответ: .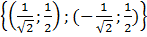

На графике функции 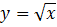найти точку 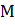, ближайшую к данной точке 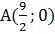. Решение.

Сделаем рисунок (см. рис.10).

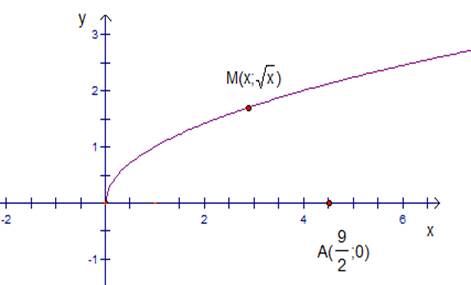
Рис. 10. График функции .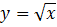

Заданы координаты двух точек: 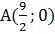и .

Найдем расстояние АМ:

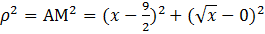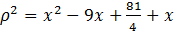или .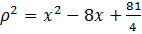

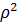— квадратичная функция от 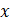. Вспомним, что нужно найти минимальное значение, то есть 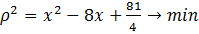. Графиком этой функции является парабола, ветвями направленная вверх, значит, минимум находится в вершине. Выделим полный квадрат и получим:

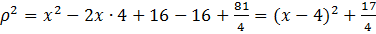. Выяснилось, что 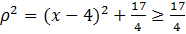. Равенство достигается, когда 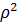принимает самое минимальное значение. Это будет в случае, когда 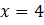. Таким образом, получили ответ 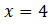, а 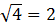. Значит, координаты точки .

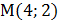Ответ: .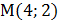

Итак, мы рассмотрели задачи на расстояние от точки до кривой. Можно находить само это расстояние, можно искать точки, которые обеспечивают минимум этого расстояния. Повторили, что такое расстояние между фигурами. Расстояние от точки до кривой – это наименьшее из расстояний, которое получается, когда точка на кривой пробегает все возможные значения. Например, точка 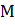может пробегать все значения на кривой 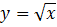, но наименьшее расстояние будет тогда, когда точка 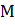имеет координаты 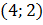. Для этого нужно, во-первых, вспомнить, что такое расстояние, и во-вторых, каким образом ищется расстояние между точками, если известны координаты. И, наконец, надо записать квадрат расстояния и проанализировать полученную функцию. Если не удается это сделать элементарными средствами, с помощью свойств квадратичной функции, то надо использовать производную и искать наименьшее значение функции .

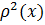Список рекомендованной литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.

8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983

Дополнительные веб-ресурсы

1. Интернет-портал Mathematics.ru (Источник).

2. Портал Естественных Наук (Источник).

3. Интернет-портал Exponenta.ru (Источник).

Сделай дома

№ 46.52 (а) (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)

interneturok.ru

Расстояние от точки до прямой в пространстве.

Формула для вычисления расстояния от точки до прямой в пространстве

Если s = {m; n; p} — направляющий вектор прямой l, M₁(x₁, y₁, z₁) — точка лежащей на прямой, тогда расстояние от точки M₀(x₀, y₀, z₀) до прямой l можно найти, используя формулу

Вывод формулы вычисления расстояния от точки до прямой в пространстве

Если задано уравнение прямой l то несложно найти s = {m; n; p} — направляющий вектор прямой и M₁(x₁, y₁, z₁) — координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах

S = |M₀M₁×s|.

С другой стороны площадь параллелограмма равна произведению его стороны на высоту проведенную к этой стороне

S = |s|d.

В нашем случае высота будет равна расстоянию от точки до плоскости d, а сторона параллелограмма равна модулю направляющего вектора s.

Приравняв площади несложно получить формулу расстояния от точки до прямой.

Примеры задач на вычисление расстояния от точки до прямой в пространстве

Пример 1.

Найти расстояние между точкой M(0, 2, 3) и прямой

x — 3	=	y — 1	=	z + 1
2	=	1	=	2

Решение.

Из уравнения прямой получим:

s = {2; 1; 2} — направляющий вектор прямой;
M₁(3; 1; -1) — точка лежащая на прямой.

Тогда

M₀M₁ = {3 — 0; 1 — 2; -1 — 3} = {3; -1; -4}

M₀M₁×s =	i	j	k	=
	3	-1	-4
	2	1	2

= i ((-1)·2 — (-4)·1) — j (3·2 — (-4)·2) + k (3·1 -(-1)·2) = {2; -14; 5}

d = |M₀M₁×s||s| = √2² + (-14)² + 5²√2² + 1² + 2² = √225√9 = 153 = 5

Ответ: расстояние от точки до прямой равно 5.

ru.onlinemschool.com

Расстояние от точки до прямой на плоскости

Расстояние от точки до прямой на плоскости — это кратчайшее расстояние от точки до прямой в евклидовой геометрии. Расстояние равно длине отрезка, который соединяет точку с прямой и перпендикулярен прямой. Формула вычисления расстояния может быть получена и выражена несколькими способами.

Знание наименьшего расстояния от точки до прямой может быть полезно во многих случаях, например, для поиска кратчайшего пути для выхода на дорогу, определение разброса графа, и подобное. В регрессии Деминга, процедуре линейного сглаживания, если зависимые и независимые переменные имеют одну и ту же дисперсию, регрессия сводится к ортогональной регрессии, в которой степень приближения измеряется для каждой точки как расстояние от точки до регрессионной прямой.

Декартова система координат

Прямая задана уравнением

Когда прямая на плоскости задана уравнением ax + by + c = 0, где a, b и c — такие вещественные константы, что a и b не равны нулю одновременно, и расстояние от прямой до точки (x₀,y₀) равно ^[1]

distance⁡(ax+by+c=0,(x0,y0))=|ax0+by0+c|a2+b2.{\displaystyle \operatorname {distance} (ax+by+c=0,(x_{0},y_{0}))={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}.}

Точка на прямой, наиболее близкая к (x₀,y₀), имеет координаты ^[2]

x=b(bx0−ay0)−aca2+b2{\displaystyle x={\frac {b(bx_{0}-ay_{0})-ac}{a^{2}+b^{2}}}} и y=a(−bx0+ay0)−bca2+b2.{\displaystyle y={\frac {a(-bx_{0}+ay_{0})-bc}{a^{2}+b^{2}}}.}

Горизонтальные и вертикальные прямые

В общем уравнении прямой ax + by + c = 0 коэффициенты a и b не могут быть одновременно равны нулю пока c не нулевое, а в случае всех нулевых коэффициентов уравнение не задаёт прямую. Если a = 0, а b ≠ 0, прямая горизонтальна и имеет уравнение y = —c/b. Расстояние от (x₀, y₀) до этой прямой определяется вертикальным отрезком длины |y₀ — (-c/b)| = |by₀ + c| / |b| (согласно формуле). Аналогичным образом, для вертикальных прямых (b = 0) расстояние между той же точкой и прямой равно |ax₀ + c| / |a| и измеряется вдоль горизонтального отрезка.

Нормированное уравнение прямой

Нормированное уравнение прямой — это уравнение вида

xcos⁡α+ysin⁡α−p=0{\displaystyle x\cos \alpha +y\sin \alpha -p=0}

Нормированное уравнение получается из общего уравнения прямой ax + by + c = 0 делением всех членов на a2+b2{\displaystyle {\sqrt {a^{2}+b^{2}}}}. Тогда расстояние от точки (x₀, y₀) до прямой равно абсолютному значению отклонения и вычисляется по формуле ^[3]^[4]

|d|=|x0cos⁡α+y0sin⁡α−p|{\displaystyle |d|=|x_{0}\cos \alpha +y_{0}\sin \alpha -p|}

Прямая задана двумя точками

Если прямая проходит через две точки P₁=(x₁,y₁) и P₂=(x₂,y₂), то расстояние от (x₀,y₀) до прямой равно:

distance⁡(P1,P2,(x0,y0))=|(y2−y1)x0−(x2−x1)y0+x2y1−y2x1|(y2−y1)2+(x2−x1)2.{\displaystyle \operatorname {distance} (P_{1},P_{2},(x_{0},y_{0}))={\frac {|(y_{2}-y_{1})x_{0}-(x_{2}-x_{1})y_{0}+x_{2}y_{1}-y_{2}x_{1}|}{\sqrt {(y_{2}-y_{1})^{2}+(x_{2}-x_{1})^{2}}}}.}

Знаменатель этого выражения равен расстоянию между точками P₁ и P₂. Числитель равен удвоенной площади треугольника с вершинами (x₀,y₀), P₁ и P₂ (см. Общая формула площади треугольника в декартовых координатах). Выражение эквивалентно h=2Ab{\textstyle h={\frac {2A}{b}}}, что может быть получено преобразованием стандартной формулы площади треугольника: A=12bh{\textstyle A={\frac {1}{2}}bh}, где b — длина стороны, а h — высота на эту сторону из противолежащей вершины.

Доказательства

Алгебраическое доказательство

Это доказательство верно, только когда прямая не является ни вертикальной, ни горизонтальной. То есть мы предполагаем, что ни a, ни b в уравнении не равны нулю.

Прямая с уравнением ax + by + c = 0 имеет наклон —a/b, так что любая прямая, перпендикулярная к заданной, имеет наклон b/a. Пусть (m, n) — точка пересечения прямой ax + by + c = 0 и перпендикулярной прямой, проходящей через точку (x₀, y₀). Прямая, проходящая через эти две точки, перпендикулярна исходной прямой, так что

y0−nx0−m=ba.{\displaystyle {\frac {y_{0}-n}{x_{0}-m}}={\frac {b}{a}}.}

Таким образом, a(y0−n)−b(x0−m)=0,{\displaystyle a(y_{0}-n)-b(x_{0}-m)=0,} и после возведения в квадрат получим:

a2(y0−n)2+b2(x0−m)2=2ab(y0−n)(x0−m).{\displaystyle a^{2}(y_{0}-n)^{2}+b^{2}(x_{0}-m)^{2}=2ab(y_{0}-n)(x_{0}-m).}

Рассмотрим,

(a(x0−m)+b(y0−n))2=a2(x0−m)2+2ab(y0−n)(x0−m)+b2(y0−n)2=(a2+b2)((x0−m)2+(y0−n)2){\displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=a^{2}(x_{0}-m)^{2}+2ab(y_{0}-n)(x_{0}-m)+b^{2}(y_{0}-n)^{2}=(a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2})}

Здесь использовано возведённое в квадрат выражение. Но

(a(x0−m)+b(y0−n))2=(ax0+by0−am−bn)2=(ax0+by0+c)2{\displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=(ax_{0}+by_{0}-am-bn)^{2}=(ax_{0}+by_{0}+c)^{2}},

так как точка (m, n) расположена на прямой ax + by + c = 0. Таким образом,

(a2+b2)((x0−m)2+(y0−n)2)=(ax0+by0+c)2{\displaystyle (a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2})=(ax_{0}+by_{0}+c)^{2}}

Из этого получаем длину отрезка между этими двумя точками:

d=(x0−m)2+(y0−n)2=|ax0+by0+c|a2+b2.{\displaystyle d={\sqrt {(x_{0}-m)^{2}+(y_{0}-n)^{2}}}={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}.} ^[5].

Геометрическое доказательство

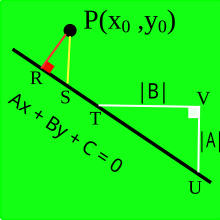
Это доказательство верно, только когда прямая не является ни вертикальной, ни горизонтальной. Баллантин и Джерберт^[6] не упомянули это ограничение в своей статье.

Опустим перпендикуляр из точки P с координатами (x₀, y₀) на прямую с уравнением Ax + By + C = 0. Обозначим основание перпендикуляра буквой R. Проведём вертикальную прямую через P и обозначим пересечение этой вертикальной прямой с исходной прямой буквой S. В произвольной точке T на прямой нарисуем прямоугольный треугольник TVU, катеты которого являются горизонтальными и вертикальными отрезками, а длина горизонтального отрезка равна |B| (см. рисунок). Вертикальный катет треугольника ∆TVU будет иметь длину |A|, поскольку наклон прямой равен —A/B.

Треугольники ∆SRP и ∆UVT подобны, так как они оба прямоугольные и ∠PSR ≅ ∠VUT, поскольку являются соответственными углами двух параллельных прямых PS и UV (вертикальные прямые) и секущей (исходная прямая)^[7]. Выпишем отношения сторон этих треугольников:

|PR¯||PS¯|=|TV¯||TU¯|.{\displaystyle {\frac {|{\overline {PR}}|}{|{\overline {PS}}|}}={\frac {|{\overline {TV}}|}{|{\overline {TU}}|}}.}

Если точка S имеет координаты (x₀,m), то |PS| = |y₀ — m| и расстояние от P до прямой равно:

|PR¯|=|y0−m||B|A2+B2.{\displaystyle |{\overline {PR}}|={\frac {|y_{0}-m||B|}{\sqrt {A^{2}+B^{2}}}}.}

Поскольку S находится на прямой, мы можем найти значение m,

m=−Ax0−CB,{\displaystyle m={\frac {-Ax_{0}-C}{B}},}

и получаем: ^[6]

|PR¯|=|Ax0+By0+C|A2+B2.{\displaystyle |{\overline {PR}}|={\frac {|Ax_{0}+By_{0}+C|}{\sqrt {A^{2}+B^{2}}}}.}

Другой вариант этого доказательства — поместить точку V в точку P и вычислить площадь треугольника ∆UVT двумя способами, после чего получим D|TU¯|=|VU¯||VT¯|{\displaystyle D|{\overline {TU}}|=|{\overline {VU}}||{\overline {VT}}|}, где D — высота треугольника ∆UVT на гипотенузу из точки P. Формула расстояния может быть использована, чтобы выразить |TU¯|{\displaystyle |{\overline {TU}}|}, |VU¯|{\displaystyle |{\overline {VU}}|} и |VT¯|{\displaystyle |{\overline {VT}}|}в терминах координат P и коэффициентов уравнения исходной прямой, в результате чего получим требуемую формулу.

Доказательство с помощью проекции вектора

Рисунок доказательства с помощью проекции вектора

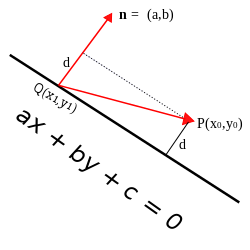
Пусть P — точка с координатами (x₀, y₀) и пусть исходная прямая имеет уравнение ax + by + c = 0. Пусть Q = (x₁, y₁) — любая точка на прямой и n — вектор (a, b) с началом в точке Q. Вектор n перпендикулярен прямой, и расстояние d от точки P до прямой равно длине ортогональной проекции QP→{\displaystyle {\overrightarrow {QP}}} на n. Длина этой проекции равна:

d=|QP→⋅n|‖n‖.{\displaystyle d={\frac {|{\overrightarrow {QP}}\cdot \mathbf {n} |}{\|\mathbf {n} \|}}.}

Теперь

QP→=(x0−x1,y0−y1),{\displaystyle {\overrightarrow {QP}}=(x_{0}-x_{1},y_{0}-y_{1}),} так что QP→⋅n=a(x0−x1)+b(y0−y1){\displaystyle {\overrightarrow {QP}}\cdot \mathbf {n} =a(x_{0}-x_{1})+b(y_{0}-y_{1})} и ‖n‖=a2+b2.{\displaystyle \|\mathbf {n} \|={\sqrt {a^{2}+b^{2}}}.}

Тогда

d=|a(x0−x1)+b(y0−y1)|a2+b2.{\displaystyle d={\frac {|a(x_{0}-x_{1})+b(y_{0}-y_{1})|}{\sqrt {a^{2}+b^{2}}}}.}

Поскольку Q лежит на прямой, c=−ax1−by1{\displaystyle c=-ax_{1}-by_{1}}, а тогда ^[8]^[9]^[10]

d=|ax0+by0+c|a2+b2.{\displaystyle d={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}.}

Другие формулы

Можно получить другие выражения для кратчайшего расстояния от точки до прямой. Эти выводы тоже требуют, чтобы прямая не была вертикальной или горизонтальной.

Пусть точка P задана координатами (x0,y0{\displaystyle x_{0},y_{0}}). Пусть прямая задана уравнением y=mx+k{\displaystyle y=mx+k}. Уравнение прямой, перпендикулярной исходной прямой и проходящей через точку P, задаётся уравнением y=x0−xm+y0{\displaystyle y={\frac {x_{0}-x}{m}}+y_{0}}.

Точка, в которой эти две прямые пересекаются, является ближайшей точкой на исходной прямой для точки P. Тогда:

mx+k=x0−xm+y0.{\displaystyle mx+k={\frac {x_{0}-x}{m}}+y_{0}.}

Мы можем решить это уравнение по x,

x=x0+my0−mkm2+1.{\displaystyle x={\frac {x_{0}+my_{0}-mk}{m^{2}+1}}.}

Координату y точки пересечения можно найти, подставив значение x в уравнение исходной прямой,

y=m(x0+my0−mk)m2+1+k.{\displaystyle y=m{\frac {(x_{0}+my_{0}-mk)}{m^{2}+1}}+k.}

Подставив полученные значения в формулу расстояния d=(X2−X1)2+(Y2−Y1)2{\displaystyle d={\sqrt {(X_{2}-X_{1})^{2}+(Y_{2}-Y_{1})^{2}}}}, получим формулу кратчайшего расстояния от точки до прямой:

d=(x0+my0−mkm2+1−x0)2+(mx0+my0−mkm2+1+k−y0)2.{\displaystyle d={\sqrt {\left({{\frac {x_{0}+my_{0}-mk}{m^{2}+1}}-x_{0}}\right)^{2}+\left({m{\frac {x_{0}+my_{0}-mk}{m^{2}+1}}+k-y_{0}}\right)^{2}}}.}

Если заметить, что m = —a/b и k = —c/b для уравнения ax + by + c = 0, после небольших выкладок получим стандартное выражение^[2].

Формулировка с помощью векторов

$d={\sqrt {\left({{\frac {x_{0}+my_{0}-mk}{m^{2}+1}}-x_{0}}\right)^{2}+\left({m{\frac {x_{0}+my_{0}-mk}{m^{2}+1}}+k-y_{0}}\right)^{2}}}.$

Иллюстрация формулировки с помощью векторов.

Запишем прямую в векторном виде:

x=a+tn{\displaystyle \mathbf {x} =\mathbf {a} +t\mathbf {n} },

где x — вектор, задающий координаты любой точки на прямой, n — единичный вектор в направлении прямой, a — вектор, задающий две координаты точки на прямой, а t — скаляр. То есть для получения точки x на прямой начинаем с точки a на прямой и двигаемся на расстояние t вдоль прямой.

Расстояние от произвольной точки p до прямой задаётся формулой

distance⁡(x=a+tn,p)=‖(a−p)−((a−p)⋅n)n‖.{\displaystyle \operatorname {distance} (\mathbf {x} =\mathbf {a} +t\mathbf {n} ,\mathbf {p} )=\|(\mathbf {a} -\mathbf {p} )-((\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} )\mathbf {n} \|.}

Эта формула геометрически строится следующим образом: a−p{\displaystyle \mathbf {a} -\mathbf {p} } — это вектор из p в точку a на прямой. Тогда (a−p)⋅n{\displaystyle (\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} } — это длина проекции на прямую, а тогда

((a−p)⋅n)n{\displaystyle ((\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} )\mathbf {n} }

— это вектор, являющийся проекцией a−p{\displaystyle \mathbf {a} -\mathbf {p} } на прямую. Тогда

(a−p)−((a−p)⋅n)n{\displaystyle (\mathbf {a} -\mathbf {p} )-((\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} )\mathbf {n} }

является компонентой вектора a−p{\displaystyle \mathbf {a} -\mathbf {p} }, перпендикулярной прямой. Следовательно, расстояние от точки до прямой равно норме этого вектора^[11]. Эта формула может быть использована и в более высоких размерностях.

Другая формулировка с помощью векторов

Если векторное пространство ортонормально, а прямая (d ) проходит через точку B и имеет вектор направления^[en] u→{\displaystyle {\vec {u}}}, то расстояние от точки A до прямой (d) равно

d(A,(d))=‖BA→∧u→‖‖u→‖{\displaystyle d(\mathrm {A} ,(d))={\frac {\left\|{\overrightarrow {\mathrm {BA} }}\wedge {\vec {u}}\right\|}{\|{\vec {u}}\|}}},

где BA→∧u→{\displaystyle {\overrightarrow {\mathrm {BA} }}\wedge {\vec {u}}} — векторное произведение векторов BA→{\displaystyle {\overrightarrow {\mathrm {BA} }}} и u→{\displaystyle {\vec {u}}}, а ‖u→‖{\displaystyle \|{\vec {u}}\|} — норма вектора u→{\displaystyle {\vec {u}}}.

См. также

Примечания

↑ Larson, Hostetler, 2007, p. 452.
↑ ¹ ² Larson, Hostetler, 2007, p. 522.
↑ Привалов, 1966, с. 67.
↑ Делоне, Райков, 1948, с. 195.
↑ Laudanski, 2014.
↑ ¹ ² Ballantine, Jerbert, 1952, с. 242–243.
↑ Если два треугольника окажутся по разные стороны от исходной прямой, эти углы будут накрест лежащими, а потому опять равными.
↑ Anton, 1994, с. 138-9.
↑ Федотов, Карпов, 2005, с. 86.
↑ Моденов, 1967, с. 152.
↑ Sunday, Dan. Lines and Distance of a Point to a Line (неопр.). // softSurfer. Проверено 6 декабря 2013.

Литература

Делоне Б. Н., Райков Д. А. Аналитическая геометрия. T. 1. — М., Л.: ОГИЗ, 1948. — 456 с.
Моденов П. С. Аналитическая геометрия. — М.: Изд-во Моск. ун-та, 1967. — 697 с.
Привалов И. И. Аналитическая геометрия. 13-е изд. — М.: Наука, 1966. — 272 с.
Федотов А. Г., Карпов Б. В. Аналитическая геометрия. — М.: МГИЭМ, 2005. — 158 с. — ISBN 5-94506-116-6.
Anton H. Elementary Linear Algebra. 7th ed. — Somerset: John Wiley & Sons, 1994. — ISBN 0-471-58742-7.
Ballantine J. P., Jerbert A. R. Distance from a Line or Plane to a Point // American Mathematical Monthly. — 1952. — Vol. 59. — P. 242—243. — DOI:10.2307/2306514.
Larson R., Hostetler R. Precalculus: A Concise Course. — Boston: Houghton Mifflin, 2007. — xvii + 526 + 102 p. — ISBN 0-618-62719-7.
Laudański L. M. Between Certainty and Uncertainty: Statistics and Probability in Five Units with Notes on Historical Origins and Illustrative Numerical Examples. — Berlin; Heidelberg: Springer Verlag, 2014. — x + 318 p. — (Intelligent Systems Reference Library, vol. 31). — ISBN 978-3-642-25696-7.

Дополнительная литература

wiki.sc

Графическое определение расстояния от точки до прямой

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.

Алгоритм

Прямую переводят в положение, в котором она будет параллельна какой-либо плоскости проекции. Для этого применяют методы преобразования ортогональных проекций.
Из точки проводят перпендикуляр к прямой. В основе данного построения лежит теорема о проецировании прямого угла.
Длина перпендикуляра определяется путем преобразования его проекций или с использованием способа прямоугольного треугольника.

Пример

На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.

Решение

Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей, который не предполагает перемещение фигур в пространстве.

Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П₄. В новой системе (П₁, П₄) точки C»₁, D»₁, M»₁ находятся на том же удалении от оси X₁, что и C», D», M» от оси X.

Выполняя вторую часть алгоритма, из M»₁ опускаем перпендикуляр M»₁N»₁ на прямую b»₁, поскольку прямой угол MND между b и MN проецируется на плоскость П₄ в натуральную величину. По линии связи определяем положение точки N’ и проводим проекцию M’N’ отрезка MN.

На заключительном этапе нужно определить величину отрезка MN по его проекциям M’N’ и M»₁N»₁. Для этого строим прямоугольный треугольник M»₁N»₁N₀, у которого катет N»₁N₀ равен разности (Y_M₁ – Y_N₁) удаления точек M’ и N’ от оси X₁. Длина гипотенузы M»₁N₀ треугольника M»₁N»₁N₀ соответствует искомому расстоянию от M до b.

Второй способ решения

Параллельно CD вводим новую фронтальную плоскость П₄. Она пересекает П₁ по оси X₁, причем X₁∥C’D’. В соответствии с методом замены плоскостей определяем проекции точек C»₁, D»₁ и M»₁, как это изображено на рисунке.
Перпендикулярно C»₁D»₁ строим дополнительную горизонтальную плоскость П₅, на которую прямая b проецируется в точку C’₂ = b’₂.
Величина расстояния между точкой M и прямой b определяется длиной отрезка M’₂C’₂, обозначенного красным цветом.

Похожие задачи:

ngeometry.ru

Расстояние от точки до прямой онлайн

С помощю этого онлайн калькулятора можно найти расстояние от точки до прямой. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до прямой, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Расстояние от точки до прямой − теория, примеры и решения

Рассмотрим эту задачу в двухмерном и трехмерном пространствах.

1. Расстояние от точки до прямой на плоскости

Пусть в двухмерном пространстве задана точка M₀(x₀, y₀) и прямая L:

где q=(m,p) направляющий вектор прямой L.

Найдем расстояние от точки M₀ до прямой (1)(Рис.1).

Алгоритм нахождения расстояния от точки M₀ до прямой L содержит следующие шаги:

построить прямую L₁, проходящую через точку M₀ и перпендикулярную прямой L,
найти пересечение прямых L и L₁(точка M₁)
найти найти расстояние между точками M₀ и M₁.

Уравнение прямой, проходящей через точку M₀(x₀, y₀) имеет следующий вид:

где n=(A,B) нормальный вектор прямой L₁.

Как видно из рисунка Рис.1, для того, чтобы прямая L₁ была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L₁, поэтому в качестве нормального вектора прямой L₁ достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L₁, представленной уравнением (2) можно записать так:

Откроем скобки

Для нахождения точки пересечения прямых L и L₁, которая и будет проекцией точки M₀ на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M₁(x₁, y₁).

Найдем точку пересечения прямых L и L₁ другим методом.

Выведем параметрическое уравнение прямой (1):

Подставим значения x и y в (4):

Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L₁(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M₀ на прямую L:

где x₁=mt’+x’, y₁=pt’+y’.

Далее находим расстояние между точками M₀ и M₁ используя формулу:

Пример 1. Найти расстояние от точки M₀(−6, 2) до прямой

Решение.

Направляющий вектор прямой (8) имеет вид:

Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M’ (x’, y’)=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x’=1, y’=7. Подставим значения m, p, x₀, y₀, x’, y’ в (6):

Подставляя значение t в (5), получим:

Вычислим расстояние между точками M₀(-6, 2) и M₁

Упростим и решим:

Ответ:

Расстояние от точки M₀(-6, 2) до прямой (8) :

2. Расстояние от точки до прямой в пространстве

Пусть в трехмерном пространстве задана точка M₀(x₀, y₀, z₀) и прямая L:

где q=(m, p, l) направляющий вектор прямой L.

Найдем расстояние от точки M₀ до прямой (9)(Рис.2).

Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:

построить плоскость α, проходящую через точку M₀ и перпендикулярную прямой L,
найти пересечение плоскости α и прямой L(точка M₁)
найти расстояние между точками M₀ и M₁.

Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) имеет следующий вид:

где n=(A,B,C) нормальный вектор плоскости α.

Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (10) можно записать так:

Откроем скобки

Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M₀ на прямую L, выведем параметрическое уравнение прямой (9):

Подставим значения x и y в (11):

Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t’ в (12) получим координаты проекции точки M₀ на прямую L:

где x₁=mt’+x’, y₁=pt’+y’, z₁=lt’+z’.

Далее вычисляем расстояние между точками M₀ и M₁ используя формулу

которое является расстоянием между точкой M₀ и прямой (9).

Пример 2. Найти расстояние от точки M₀(1, 2, 1) до прямой

Решение.

Направляющий вектор прямой (15) имеет вид:

Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M’ (x’, y’, z’)=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x’=4, y’=3, z’=1. Подставим значения m, p, l x₀, y₀, z₀ x’, y’, z’ в (13):

Подставляя значение t=t’ в (12), получим координаты точки M₁:

Далее, используя формулу (14) вычисляем расстояние от точки M₀ до прямой (15):

Упростим и решим:

Ответ:

Расстояние от точки M₀(1, 2, 1) до прямой (15) :

matworld.ru

расстояние — это… Что такое расстояние?

Морфология: (нет) чего? расстоя́ния, чему? расстоя́нию, (вижу) что? расстоя́ние, чем? расстоя́нием, о чём? о расстоя́нии; мн. что? расстоя́ния, (нет) чего? расстоя́ний, чему? расстоя́ниям, (вижу) что? расстоя́ния, чем? расстоя́ниями, о чём? о расстоя́ниях

1. Расстоянием называется промежуток между кем-либо, чем-либо, пространство, разделяющее два пункта, два объекта. Кратчайшее расстояние между двумя точками. | Расстояние от дома до школы. | Расстояние от пункта А до пункта Б.
2. Расстоянием называется удалённость одного объекта от другого. Стоять на расстоянии пяти шагов от кого-либо. | Отойти на близкое, некоторое расстояние от кого-либо. | Располагать что-либо на равном, одинаковом расстоянии от чего-либо. | Звуки слышны на расстоянии. | Луна находится на расстоянии в 60 земных радиусов от Земли.
3. Если какое-либо действие имеет место, происходит на расстоянии, то это означает, что кто-либо производит какие-либо действия, манипуляции объектами, находясь в удалении от них, не будучи рядом. Общаться с кем-либо на расстоянии. | Владелец может включать и выключать сигнализацию на расстоянии.
4. Расстоянием называется отрезок пути, часть какой-либо длины. Пройти расстояние в пять километров. | Пробежать порядочное, большое, короткое расстояние. | Ездить, летать на большие расстояния.
5. Если кто-либо держит кого-либо на расстоянии, то это означает, что этот человек не даёт другому человеку, животному приблизиться, подойти к себе. Держите противника на расстоянии.

6. Если кто-либо держит кого-либо на почтительном расстоянии, то это означает, что этот человек не допускает другого человека до сближения с собой, не хочет с ним общаться.

dic.academic.ru